2022-2023學年浙江省9+1高中聯盟高一（上）期中數學試卷

一、選擇題（本大題共8題，每小題5分，共40分.每小題列出的四個備選項中只有一個是符合題目要求的，不選、多選、錯選均不得分）

• 1．已知集合A={0，2，4}，B={x|x（x-3）≤0}，則A∩B=（　　）

  A．{0，2}

  B．{2，4}

  C．{0，2，4}

  D．{2}
  組卷：39引用：4難度：0.8

  解析

• 2．命題“?x∈R，?n∈N*，使得n≤x”的否定形式是（　　）

  A．?x∈R，?n∈N*，使得n＞x	B．?x∈R，?n∈N*，都有n＞x
  C．?x∈R，?n∈N*，使得n＞x	D．?x∈R，?n∈N*，都有n＞x
  組卷：372引用：8難度：0.7

  解析

• 3．“x²＞x”是“x＜-1”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：64引用：3難度：0.8

  解析

• 4．設f（x）是定義域為R上的偶函數，且在（0，+∞）上單調遞增，則（　　）

  A．f（50.3）＞f（- 5 ）＞f（0.35）

  B．f（- 5 ）＞f（0.35）＞f（50.3）

  C．f（0.35）＞f（50.3）＞f（- 5 ）

  D．f（- 5 ）＞f（50.3）＞f（0.35）
  組卷：22引用：1難度：0.5

  解析

• 5．某商場在國慶期間舉辦促銷活動，規定：顧客購物總金額不超過400元，不享受折扣；若顧客的購物總金額超過400元，則超過400元部分分兩檔享受折扣優惠，折扣率如表所示：
  

  可以享受折扣優惠金額	折扣率
  不超過400元部分	5%
  超過400元部分	15%

  若某顧客獲得65元折扣優惠，則此顧客實際所付金額為（　　）

  A．935元

  B．1000元

  C．1035元

  D．1100元
  組卷：83引用：4難度：0.5

  解析

• 6．若

  a

  ∈

  {

  1

  2

  ，

  2

  ，

  3

  }

  ，則函數f（x）=a^|x|與g（x）=x^a的部分圖像不可能是（　　）

  A．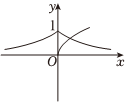

  B．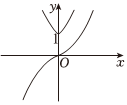

  C．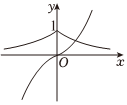

  D．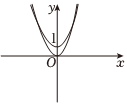
  組卷：29引用：3難度：0.7

  解析

• 7．已知函數f（x），g（x）的定義域為R，設

  f

  （

  x

  ）

  =

  1

  +

  1

  -

  e

  x

  1

  +

  e

  x

  ，且g（x）-1是奇函數，若函數f（x）與g（x）的圖像的交點坐標分別為（x₁，y₁），（x₂，y₂），（x₉，y₉），則（x₁+x₂+…+x₉）（y₁+y₂+…+y₉）=（　　）

  A．0

  B．-8

  C．8

  D．9
  組卷：53引用：2難度：0.6

  解析

四、解答題（本大題共6題，共70分.解答應寫出文字說明、證明過程或演算步驟）

• 21．設函數

  f

  （

  x

  ）

  =

  x

  +

  a

  4

  x

  2

  -

  1

  ，

  a

  ∈

  R

  ．
  （1）討論函數f（x）的奇偶性（寫出結論，不需要證明）；
  （2）是否存在實數a,使得關于x的方程

  f

  （

  1

  2

  x

  +

  1

  ）

  =

  1

  有唯一解？若存在，求出實數a的取值范圍：若不存在，請說明理由．
  組卷：70引用：2難度：0.5

  解析

• 22．設函數

  f

  （

  x

  ）

  =

  x

  2

  +

  1

  x

  2

  +

  ax

  +

  a

  x

  +

  b

  ,

  a

  ,

  b

  ∈

  R

  ．
  （1）當a=0時，判斷f（x）在（0，1）上的單調性，并用定義法證明；
  （2）對?a∈[-4，+∞]及b∈R，總存在x₀∈[1，2]，使得|f（x₀）|≥t成立，求實數t的取值范圍．
  組卷：74引用：2難度：0.5

  解析