2010年初二奧數培訓22：幾何不等式

一、解答題（共16小題，滿分0分）

• 1．在銳角三角形ABC中，AB＞AC，AM為中線，P為△AMC內一點，證明：PB＞PC（如圖）．
  組卷：513引用：3難度：0.7

  解析

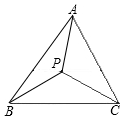• 2．已知P是△ABC內任意一點（如圖）．
  （1）求證：

  1

  2

  （a+b+c）＜PA+PB+PC＜a+b+c；
  （2）若△ABC為正三角形，且邊長為1，求證：PA+PB+PC＜2．
  組卷：153引用：2難度：0.9

  解析

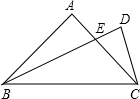• 3．如圖，已知在線段BC同側作兩個三角形△ABC和△DBC，使AB=AC，DB＞DC且AB+AC=DB+DC，設AC與DB交于E．
  求證：AE＞DE．
  組卷：243引用：3難度：0.9

  解析

• 4．設G是正方形ABCD的邊DC上一點，連接AG并延長交BC延長線于K，求證：

  1

  2

  （AG+AK）＞AC．
  組卷：61引用：1難度：0.5

  解析

• 5．如圖．設BC是△ABC的最長邊，在此三角形內部任選一點O，AO，BO，CO分別交對邊于A′，B′，C′．
  證明：（1）OA′+OB′+OC′＜BC；
  （2）OA′+OB′+OC′≤max{AA′，BB′，CC′}．
  組卷：37引用：1難度：0.7

  解析

一、解答題（共16小題，滿分0分）

• 15．在△ABC中，AB＞AC，AD為高，P為AD上的任意一點，求證：PB-PC＞AB-AC．
  組卷：194引用：1難度：0.3

  解析

• 16．在等腰△ABC中，AB=AC．
  （1）若M是BC的中點，過M任作一直線交AB，AC（或其延長線）于D，E，求證：2AB＜AD+AE．
  （2）若P是△ABC內一點，且PB＜PC，求證：∠APB＞∠APC．
  組卷：92引用：1難度：0.5

  解析