2021-2022學年陜西省渭南市澄城縣高一（下）期末數學試卷（C卷）

一、選擇題（本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．為調查參加考試的高二級1200名學生的成績情況，從中抽查了100名學生的成績，就這個問題來說，下列說法正確的是（　　）

  A．1200名學生是總體

  B．每個學生是個體

  C．樣本容量是100

  D．抽取的100名學生是樣本
  組卷：227引用：3難度：0.8

  解析

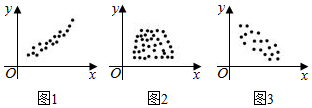• 2．觀察下列散點圖，則①正相關，②負相關，③不相關，這三句話與散點圖的位置相對應的是（　　）

  A．①②③

  B．②③①

  C．②①③

  D．①③②
  組卷：226引用：11難度：0.9

  解析

• 3．下列事件中，是隨機事件的是（　　）
  ①經過有交通信號燈的路口，剛好是紅燈；
  ②投擲2顆質地均勻的骰子，點數之和為14；
  ③拋擲一枚質地均勻的硬幣，字朝上；
  ④13個人中至少有2個人的生日在同一個月．

  A．①③

  B．③④

  C．①④

  D．②③
  組卷：155引用：1難度：0.7

  解析

• 4．要考察某公司生產的500克袋裝牛奶的質量是否達標，現從500袋牛奶中抽取50袋進行檢驗，將它們編號為000，001，002，…499，利用隨機數表抽取樣本，從第8行第5列的數開始，按3位數依次向右讀取，到行末后接著從下一行第一個數繼續．則第三袋牛奶的標號是（　　）
  （下面摘取了某隨機數表的第7行至第9行）
  84421  75331  57245  50688  77047  44767  21763
  35025  83921  20676  63016  47859  16955  56719
  98105  07185  12867  35807  44395  23879  33211

  A．358

  B．169

  C．455

  D．206
  組卷：332引用：3難度：0.8

  解析

• 5．將兩個數a=1，b=2交換，使a=2，b=1，下列語句正確的是（　　）

  A．a=c,c=b,b=a	B．c=b,b=a,a=c
  C．a=b,b=a	D．b=a,a=b
  組卷：26引用：1難度：0.8

  解析

• 6．有一組樣本數據x₁，x₂，…，x_n，由這組數據得到新樣本數據y₁，y₂，…，y_n，其中y_i=x_i+c（i=1，2，…，n），c≠0，則這兩組樣本數據的（　　）

  A．平均數相同

  B．標準差相同

  C．中位數相同

  D．眾數相同
  組卷：182引用：6難度：0.8

  解析

• 7．把紅、黃、藍、綠4張紙牌隨機地分發給甲、乙、丙、丁四人，每個人分得一張，事件“甲分得藍牌”與“丁分得藍牌”（　　）

  A．是對立事件	B．是不可能事件
  C．不是互斥事件	D．是互斥但不對立事件
  組卷：75引用：1難度：0.9

  解析

三、解答題（本大題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟）

• 21．某單位從一所學校招收某類特殊人才．對20位已經選拔入圍的學生進行運動協調能力和邏輯思維能力的測試，其測試結果如下表：
  

  邏輯思維能力 運動協調能力	一般	良好	優秀
  一般	2	2	1
  良好	4	b	1
  優秀	1	3	a

  例如表中運動協調能力良好且邏輯思維能力一般的學生是4人．由于部分數據丟失，只知道從這20位參加測試的學生中隨機抽取一位，抽到邏輯思維能力優秀的學生的概率為

  1

  5

  ．
  （Ⅰ）求a,b的值；
  （Ⅱ）從運動協調能力為優秀的學生中任意抽取2位，求其中至少有一位邏輯思維能力優秀的學生的概率．
  組卷：142引用：6難度：0.5

  解析

• 22．為有效防控疫情，于2021年9月開始，多省份相繼啟動新冠疫苗加強免疫接種工作．新冠疫苗接種一段時間后，有保護效果削弱的情況存在，加強針的接種則會使這種下降出現“強勢反彈”．研究結果顯示，接種加強針以后，受種者的抗體水平將大幅提升，加強免疫14天后，抗體水平相當于原來的10-30倍，6個月后，能維持在較高水平，并且對德爾塔等變異株出現良好交叉中和作用．
  某市開展加強免疫接種工作以來，在某一周的接種人數（單位：萬人）如下表所示：
  

  	星期一	星期二	星期三	星期四	星期五	星期六	星期天
  當日接種人數y（萬人）	1.7	1.9	2.1	2.3	2.4	2.5	a

  設天數為x（x=1，2，3，4，5，6，7），規定星期一為x=1．
  （Ⅰ）若y與x（x=1，2，3，4）具有線性相關關系，求y關于x的線性回歸方程；
  （Ⅱ）根據（Ⅰ）中所求的線性回歸方程分別計算星期五，星期六的預報值

  ?

  y

  ，并與當日接種人數的真實值y進行比較．若都滿足

  |

  ?

  y

  -

  y

  |

  ≤

  0

  .

  1

  ，則可用此線性回歸方程預測以后的接種人數．請判斷（I）中所求的線性回歸方程是否可以預測以后的接種人數？若可預測，請預測星期日的接種人數a；若不可預測，請說明理由．
  參考公式：

  ?

  b

  =

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  （

  y

  i

  -

  y

  ）

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  2

  =

  n

  ∑

  i

  =

  1

  x

  i

  y

  i

  -

  n

  x

  y

  n

  ∑

  i

  =

  1

  x

  2

  i

  -

  n

  2

  ，

  ?

  a

  =

  y

  -

  ?

  b

  x

  ．
  組卷：20引用：1難度：0.5

  解析