2023-2024學年四川省眉山市仁壽縣華興中學八年級（上）入學數學試卷

一、選擇題

• 1．若a＜b,下列不等式不一定成立的是（　　）

  A．a-2＜b-2

  B．-2a＞-2b

  C． a 2 ＜ b 2

  D．ac2＞bc2
  組卷：48引用：2難度：0.8

  解析

• 2．如果x=1是關于x的方程3x+4m-7=0的解，則m的值是（　　）

  A．1

  B．-1

  C．6

  D．-6
  組卷：112引用：3難度：0.8

  解析

• 3．在以下綠色食品、回收、節能、節水四個標志中，是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：5228引用：206難度：0.9

  解析

• 4．若一個正多邊形的一個內角等于150°，則這個正多邊形的邊數是（　　）

  A．9

  B．10

  C．11

  D．12
  組卷：481引用：12難度：0.9

  解析

• 5．用邊長相等的兩種正多邊形進行密鋪，其中一種是正八邊形，則另一種正多邊形可以是（　　）

  A．正三角形

  B．正方形

  C．正五邊形

  D．正六邊形
  組卷：418引用：8難度：0.7

  解析

• 6．如果等腰三角形的兩邊長分別為2和5，則它的周長為（　　）

  A．9

  B．7

  C．12

  D．9或12
  組卷：410引用：52難度：0.9

  解析

• 7．若

  x = 3 - m

  y = 1 + 2 m

  則y用含x的代數式表示為（　　）

  A．y=2x+7

  B．y=-2x+7

  C．y=2x-5

  D．y=-2x-5
  組卷：336引用：4難度：0.7

  解析

• 8．方程

  x

  -

  x

  -

  1

  2

  =

  x

  +

  2

  3

  去分母，正確的是（　　）

  A．6x-3（x-1）=x+2	B．6x-3（x-1）=2（x+2）
  C．x-3（x-1）=2（x+2）	D．x-（x-1）=2（x+2）
  組卷：1736引用：12難度：0.9

  解析

三、解答題：

• 25．感悟思想：
  有些關于方程組的問題，欲求的結果不是每一個未知數的值，而是關于未知數的代數式的值，如以下問題：
  已知實數x,y滿足3x-y=5①，2x+3y=7②，求x-4y和7x+5y的值．
  思考：本題常規思路是將①②聯立成方程組，解得x,y的值再代入欲求值的代數式得到答案，有的問題用常規思路運算量比較大．其實，仔細觀察兩個方程未知數的系數之間的關系，本題還可以通過適當變形整體求得代數式的值．
  如①-②可得x-4y=-2①+②×2可得7x+5y=19．
  這樣的解題思想就是通常所說的“整體思想”．
  體會思想：
  （1）已知二元一次方程組

  2 x + y = 7

  x + 2 y = 8

  ，則x-y=

  ，x+y=

  ．
  （2）解方程組：

  x + y = 5

  x + z = 3

  y + z = 4

  ．
  （3）某班級組織活動購買小獎品，買20支鉛筆、3塊橡皮、2本日記本共需32元，買39支鉛筆5塊橡皮、3本日記本共需58元，則購買5支鉛筆、5塊橡皮、5本日記本共需多少元？
  組卷：89引用：4難度：0.5

  解析

• 26．如圖1，已知直線EF∥GH，且EF和GH之間的距離為1，小李同學制作了一個直角三角形硬紙板ACB，其中∠ACB=90°，∠BAC=60°，AC=1．小李利用這塊三角板進行了如下的操作探究：
  （1）如圖1，若點C在直線EF上，且∠ACE=15°，求∠1的度數；
  （2）若點A在直線EF上，點C在EF和GH之間（不含EF、GH上），邊BC、AB與直線GH分別交于點D和點K．
  ①如圖2，KO平分∠BKD，DO平分∠BDK，KO與DO交于點O．在△ABC繞著點A旋轉的過程中，∠KOD的度數是否會發生變化？如果不發生變化，請求出∠KOD的度數；如果發生變化，請說明理由；
  ②如圖3，在△ABC繞著點A旋轉的過程中，設∠EAK=n°，∠CDK=（3m-2n+15）°，求m的取值范圍．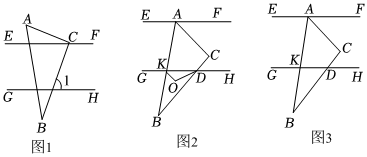
  ?
  組卷：140引用：4難度：0.5

  解析