2020-2021學年山東省濰坊市高一（下）期中數學試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一-項是符合題目要求的.

• 1．角2021°的終邊所在的象限為（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：60引用：2難度：0.8

  解析

• 2．函數f（x）=lg（tanx-1）的定義域為（　　）

  A．{x|x≠kπ+ π 2 ，k∈Z}	B．{x|kπ- π 2 ＜x＜kπ+ π 2 ，k∈Z}
  C．{x|kπ＜x＜kπ+ π 2 ，k∈Z}	D．{x|kπ+ π 4 ＜x＜kπ+ π 2 ，k∈Z}
  組卷：632引用：2難度：0.8

  解析

• 3．在現代社會中，信號處理是非常關鍵的技術，而信號處理背后的“功臣”就是正弦型函數．若某種信號的波形對應的函數解析式為f（x）=sinx+

  1

  3

  sin

  x

  3

  ，則其部分圖像為（　　）

  A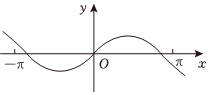．	B．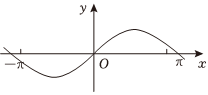
  C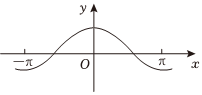．	D．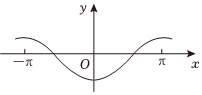
  組卷：50引用：2難度：0.6

  解析

• 4．若α∈（-

  π

  2

  ，0），則

  1

  -

  sin

  2

  α

  =（　　）

  A．sinα+cosα

  B．-sinα-cosα

  C．sinα-cosα

  D．cosα-sinα
  組卷：31引用：2難度：0.7

  解析

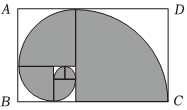• 5．斐波那契螺旋線被譽為自然界最完美的“黃金螺旋”，它的畫法是：以斐波那契數1，1，2，3，5，8…作為正方形的邊長拼成長方形，然后在每個正方形中畫一個圓心角為90°的圓弧，這些圓弧所連起來的弧線就是斐波那契螺旋線．如圖這些圓弧所連成的弧線就是斐波那契螺旋線的前一部分，則陰影部分的面積與矩形ABCD的面積之比為（　　）

  A． 3 4

  B． 1 4

  C． π 4

  D． π 8
  組卷：17引用：1難度：0.7

  解析

• 6．如圖，在矩形ABCD中，

  AB

  =

  a

  ，

  AD

  =

  b

  ，M為CD的中點，BD與AM交于點N，則

  MN

  =（　　）

  A．- 1 6 a - 1 3 b

  B． 1 6 a - 1 3 b

  C． 1 6 a + 1 3 b

  D．- 1 6 a + 1 3 b
  組卷：103引用：3難度：0.6

  解析

• 7．已知0＜α＜β＜

  π

  2

  ，cos（α-β）=

  4

  5

  ，sinβ=

  2

  2

  ，則sinα=（　　）

  A． 2 10

  B． 7 2 10

  C．- 2 10

  D．- 7 2 10
  組卷：34引用：3難度：0.7

  解析

四、解答題：本大題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

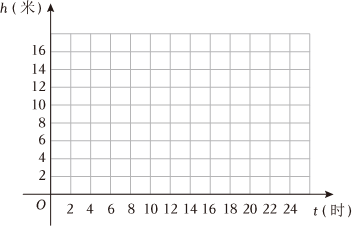• 21．潮汐現象是發生在沿海地區的一種自然現象，是指海水在天體（主要是月球和太陽）引潮力作用下所產生的周期性運動，我們把海面垂直方向漲落稱為潮汐，地球上不同的地點潮汐規律不同．
  如表給出了某沿海港口在一天（24小時）中海水深度的部分統計數據：
  

  時間t（時）	0	2	4	6	8	10	12
  水深h（米）	13.4	14	13.4	12	10	8	6.6
  時間t（時）	14	16	18	20	22	24
  水深h（米）	6	6.6	8	10	12	13

  （1）請結合表中數據，在給出的平面直角坐標系中，選擇合適的點，畫出該港口在一天24小時中海水深度h與時間t的函數圖像，并根據你所學知識，請從h（t）=at²+bt+c（a＞0）．h（t）=2^t，h（t）=Asin（ωt+φ）+B（A＞0，?＞0，|φ|＜

  π

  2

  ），h（t）=Acos（ωt+φ）+B （A＞0，?＞0，|φ|＜

  π

  2

  ）這四個函數解析式中，選取一個合適的函數模型描述該港口一天24小時內水深h與時間t的函數關系，求出其解析式；
  （2）現有一貨輪需進港卸貨，并在白天進行物資補給后且于當天晚上離港．已知該貨輪進港時的吃水深度（水面到船底的距離）為10米，卸貨后吃水深度減小0.8米，根據安全航行的要求，船底至少要留出2.8米的安全間隙（船底到海底的距離），如果你是船長，請你規劃貨輪的進港、離港時間，并計算出貨輪在該港口停留的最短時長．（參考數據；

  2

  ≈

  1.4，

  3

  ≈1.7）
  組卷：38引用：1難度：0.4

  解析

• 22．已知函數f（x）=2sin

  x

  2

  cos

  x

  2

  +2

  3

  cos²

  x

  2

  -

  3

  ．
  （1）求函數f（x）的周期；
  （2）若不等式|f（x）-m|≤3對任意x∈[-

  π

  6

  ，

  π

  3

  ]恒成立，求整數m的最大值；
  （3）若函數g（x）=f（

  π

  2

  -x），將函數g（x）的圖像上各點的橫坐標縮短到原來的

  1

  2

  倍（縱坐標不變），再向右平移

  π

  12

  個單位，得到函數y=h（x）的圖像，若關于x的方程

  1

  2

  h（x）-k（sinx+cosx）=0在x∈[-

  π

  12

  ，

  5

  π

  12

  ]上有解，求實數k的取值范圍．
  組卷：161引用：4難度：0.6

  解析