2021-2022學年河南省駐馬店市上蔡縣八年級（下）期中數學試卷

一、選擇題（每小題3分，共計30分）

• 1．要使分式

  1

  x

  -

  2

  有意義，則x的取值范圍為（　　）

  A．x≠2

  B．x=2

  C．x＞2

  D．x＜2
  組卷：251引用：5難度：0.7

  解析

• 2．把分式方程

  1

  x

  -

  2

  =

  1

  -

  x

  2

  -

  x

  化為整式方程，正確的是（　　）

  A．-（1-x）=1	B．1+（1-x）=1
  C．1-（1-x）=x-2	D．1+（1-x）=x-2
  組卷：15引用：1難度：0.7

  解析

• 3．新冠病毒是一種新的Sarbecovirus亞屬的β冠狀病毒，它是一類具有囊膜的正鏈單股RNA病毒，其遺傳物質是所有RNA病毒中最大的，也是自然界廣泛存在的一大類病毒．其粒子形狀并不規則，直徑約60～220nm,平均直徑為100nm,已知1m=10⁹nm,則100nm可以表示為（　　）

  A．0.1×10-6m

  B．10×10-8m

  C．1×10-7m

  D．1×10-11m
  組卷：6引用：1難度：0.9

  解析

• 4．甲、乙二人從鄭州出發到西安，甲乘坐高鐵，乙乘坐普通列車，結果甲比乙少用5h.已知高鐵的平均速度比普通列車快180km/h,求高鐵、普通列車的平均速度分別是多少．假設從鄭州到西安的高鐵、普通列車線路長均為520km,高鐵的平均速度為x km/h,則根據題意可列方程為（　　）

  A． 520 x = 520 x - 180 +5	B． 520 x = 520 x + 180 +5
  C． 520 x = 520 x - 180 -5	D． 520 x = 520 x + 180 -5
  組卷：664引用：4難度：0.6

  解析

• 5．已知A、B兩地相距3km,小華從A地到B地平均速度為4km/h,若用x表示行走的時間（h），y表示余下的路程（km），則y關于x的函數表達式是（　　）

  A．y=4x（x≥0）	B．y=4x-3（x≥ 3 4 ）
  C．y=3-4x（x≥0）	D．y=3-4x（0≤x≤ 3 4 ）
  組卷：83引用：2難度：0.5

  解析

• 6．在平面直角坐標系中，將點A（-3，-2）向右平移5個單位長度得到點B，則點B關于y軸對稱點B′的坐標為（　　）

  A．（2，2）

  B．（-2，2）

  C．（-2，-2）

  D．（2，-2）
  組卷：1717引用：15難度：0.7

  解析

• 7．已知將一次函數y=2x-1的圖象向上平移2個單位長度后得到y=kx+b,則下列關于一次函數y=kx+b的圖象說法正確的是（　　）

  A．經過第一、二、四象限	B．與x軸交于點（1，0）
  C．與y軸交于點（0，1）	D．y隨著x的增大而減小
  組卷：63引用：2難度：0.7

  解析

三、解答題（共計75分）

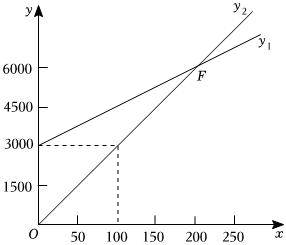• 22．某商場為了提高銷售人員的積極性，對原有的薪酬計算方式進行了修改．設銷售人員一個月的銷售量為x（件），銷售人員的月收入為（元），原有的薪酬計算方式y₁（元）采用的是底薪加上提成的方式，且y₁=k₁x+b,已知每銷售一件商品可獲得15元的提成．修改后的薪酬計算方式為y₂（元），且y₂=k₂x,根據圖象回答下列問題：
  （1）求y₁和y₂的解析式，并說明b的實際意義；
  （2）求兩個函數圖象的交點F的坐標，并說明交點F的實際意義；
  （3）根據函數圖象，請判斷哪種薪酬計算方式更適合銷售人員．
  組卷：27引用：1難度：0.5

  解析

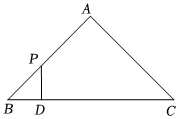• 23．如圖，△ABC是等腰直角三角形，∠A=90°，BC=4cm,點P在△ABC的邊上沿路徑B→A→C移動，過點P作PD⊥BC于點D．設BD=x cm,△BDP的面積為y cm²（當點P與點B或點C重合時，y的值為0）．
  小華根據學習函數的經驗，對函數y隨著自變量x的變化而變化的規律進行了探究．下面是小華的探究過程，請補充完整：
  （1）自變量x的取值范圍是

  ．
  （2）通過取點、畫圖、測量，得到了x與y的幾組值，如下表：
  

  x（cm）	0	1 2	1	3 2	2	5 2	3	7 2	4
  y（cm2）	0	1 8	m	9 8	2	15 8	3 2	n	0

  請直接寫出m=

  ，n=

  ．
  （3）如圖，在平面直角坐標系中，描出以補完后的表中各對對應值為坐標的點，并用平滑的曲線畫出該函數的圖象．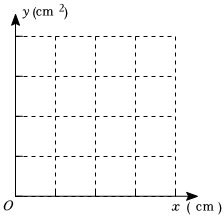
  
  （4）結合畫出的函數圖象，解決問題：當△BDP的面積為1cm²時，BD的長度約為

  （數值保留一位小數）．
  組卷：149引用：1難度：0.6

  解析