2023年陜西省咸陽市三原縣中考數學二模試卷

一、選擇題（共7小題，每小題3分，計21分.每小題只有一個選項是符合題意的）

• 1．在0、

  1

  3

  、-1、

  6

  這四個數中，最小的數是（　　）

  A．0

  B． 1 3

  C．-1

  D． 6
  組卷：38引用：4難度：0.8

  解析

• 2．計算機層析成像（CT）技術的工作原理與幾何體的切截相似，只不過這里的“截”不是真正的截，“幾何體”是病人的患病器官，“刀”是射線．如圖，用一個平行于圓錐底面的平面截圓錐，截面的形狀是（　　）

  A．

  B．

  C．

  D．
  組卷：470引用：10難度：0.8

  解析

• 3．我國古代數學家祖沖之推算出π的近似值為

  355

  113

  ，它與π的誤差小于0.0000003．將0.0000003用科學記數法可以表示為（　　）

  A．3×10-7

  B．0.3×10-6

  C．3×10-6

  D．3×107
  組卷：1509引用：28難度：0.7

  解析

• 4．如圖是小穎0到12時的心跳速度變化圖，在這一時段內心跳速度最快的時刻約為（　　）
  

  A．3時

  B．6時

  C．9時

  D．12時
  組卷：266引用：9難度：0.8

  解析

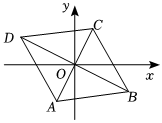• 5．如圖，菱形ABCD的對角線交于原點O，若點B的坐標為（4，m），點D的坐標為（n,2），則m+n的值為（　　）

  A．2

  B．-2

  C．6

  D．-6
  組卷：1782引用：15難度：0.8

  解析

• 6．如圖，在半徑為5的⊙O中，AB是直徑，AC是弦，D是

  ?

  AC

  的中點，AC與BD交于點E．若

  BE

  DE

  =

  1

  2

  ，則AC的長為（　　）

  A． 4 2

  B． 4 3

  C． 4 5

  D． 4 6
  組卷：780引用：7難度：0.5

  解析

• 7．已知拋物線y=ax²+bx+c與x軸的公共點是（-4，0），（2，0），將該拋物線向右平移3個單位長度與y軸的交點坐標為（0，-5），則a+b+c的值為（　　）

  A．5

  B．-5

  C．4

  D．-9
  組卷：164引用：1難度：0.6

  解析

二、填空題（共5小題，每小題3分，計15分）

• 8．計算：（

  7

  -1）（

  7

  +1）=

  ．
  組卷：160引用：2難度：0.9

  解析

三、解答題（共13小題，計84分.解答應寫出過程）

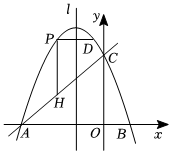• 24．如圖，已知拋物線y=-

  3

  4

  x²+bx+c與x軸交于點A（-4，0）、B（1，0），與y軸交于點C，拋物線的對稱軸為直線l,點P是直線l左側拋物線上一點且點P在x軸上方．
  （1）求拋物線的函數表達式；
  （2）過點P作x軸的平行線交拋物線于另一點D，過點P作y軸的平行線交AC于點H，求PD+PH的最大值及此時點P的坐標．
  組卷：209引用：2難度：0.6

  解析

• 25．【問題初探】：（1）如圖①，在△ABC中，點D、E分別在邊AB、AC上，連接DE，DE∥BC，AD=2DB．若DE=4，則BC的長為

  ；
  【問題深入】：（2）如圖②，在扇形OAB中，點C是

  ?

  AB

  上一動點，連接AC，BC，∠AOB=120°，OA=2，求四邊形OACB的面積的最大值；
  【拓展應用】：（3）為進一步促進西安市文化和旅游高質量發展，推動全市文明旅游創建工作，結合2023年陜西省文明旅游示范單位申報工作，一并開展2023年西安市文明旅游示范單位評選工作．某地為參加評選積極改善環境，擬建一個四邊形休閑廣場ABCD，其大致示意圖如圖③所示，其中AD∥BC，BC=120米．點E處設立一個自動售貨機，點E是BC的中點，連接AE，BD，AE與BD交于點M，連接CM，沿CM修建一條石子小路（寬度不計），將△MBE和△MDA進行綠化．根據設計要求，

  BM

  =

  2

  DM

  ，

  tan

  ∠

  CME

  =

  3

  4

  ．為倡導綠色新風尚，現要使綠化的面積盡可能的大，請問△MBE和△MDA的面積之和是否存在最大值？若存在，請求出△MBE和△MDA面積之和的最大值；若不存在，請說明理由．
  
  組卷：371引用：3難度：0.2

  解析