2022-2023學年陜西省西安市灞橋區鐵一中陸港學校九年級（上）月考數學試卷（12月份）

一.選擇題（共8小題，每小題3分，計24分）

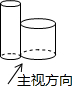• 1．如圖所示的物體由兩個緊靠在一起的圓柱體組成，它的左視圖是（　　）

  A．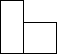

  B．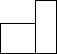

  C．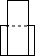

  D．
  組卷：271引用：13難度：0.9

  解析

• 2．下列函數中，是二次函數的是（　　）

  A．y=-4x+5	B．y=2x2-3x
  C．y=x（x+1）-x2	D．y= 1 x 2
  組卷：307引用：3難度：0.9

  解析

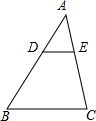• 3．如圖，DE∥BC，AD：DB=2：3，EC=6，則AE的長是（　　）

  A．3

  B．4

  C．6

  D．10
  組卷：1046引用：14難度：0.9

  解析

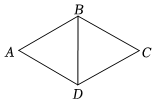• 4．如圖，在菱形ABCD中，∠BAD=60°，對角線BD=6，則菱形的邊AB的長為（　　）

  A．4

  B．6

  C．3 3

  D．8
  組卷：718引用：6難度：0.7

  解析

• 5．學生冬季運動裝原來每套的售價是100元，后經連續兩次降價，現在的售價是81元，則平均每次降價的百分數是（　　）

  A．9%

  B．8.5%

  C．9.5%

  D．10%
  組卷：237引用：34難度：0.9

  解析

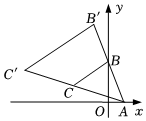• 6．如圖所示，在直角坐標系中，A（1，0），B（0，2），以A為位似中心，把△ABC按相似比1：2放大，放大后的圖形記作△AB'C'，則B'的坐標為（　　）

  A．（-1，-2）

  B．（-1，2）

  C．（-1，-4）

  D．（-1，4）
  組卷：289引用：3難度：0.6

  解析

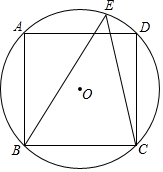• 7．如圖，正方形ABCD內接于⊙O，點E在

  ?

  AD

  上，則∠BEC的度數（　　）

  A．25°

  B．50°

  C．45°

  D．100°
  組卷：369引用：4難度：0.6

  解析

• 8．已知二次函數y=ax²+bx+c（a,b,c是常數，a≠0）的y與x的部分對應值如表：

  x	-5	-4	-2	0	2
  y	6	0	-6	-4	6

  則下列說法正確的是（　　）

  A．a＜0

  B．當x=-2時，函數最小值為-6

  C．若點（-8，y1），點（8，y2）在二次函數圖象上，y1＞y2

  D．方程ax2+bx+c+5=0有兩個不相等的實數根
  組卷：55引用：2難度：0.5

  解析

三.解答題（共12小題，計81分）

• 24．已知拋物線

  y

  =

  -

  1

  2

  x

  2

  +

  bx

  +

  c

  與x軸交于A（-1，0），B（4，0）兩點，與y軸交于點C．
  （1）求該拋物線的表達式；
  （2）求△ABC的面積；
  （3）在拋物線上是否存在一點P，使tan∠BAP=1，若存在，求出點P的坐標，若不存在，請說明理由．
  組卷：56引用：2難度：0.5

  解析

• 25．【問題提出】
  
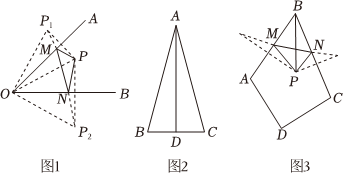
  （1）如圖1，∠AOB=45°，在∠AOB內部有一點P，M、N分別是OA、OB上的動點，分別作點P關于邊OA、OB的對稱點P₁，P₂，連接P₁，P₂與OA、OB相交于M、N，則此時△PMN的周長最小，且順次連接O，P₁，P₂后△OP₁P₂的形狀是等腰直角三角形．理由如下：
  ∵點P關于邊OA、OB的對稱點分別為P₁，P₂，
  ∴OP=OP₁=OP₂，∠AOP=∠AOP₁，∠BOP=∠BOP₂，PM=P₁M，PN=P₂N．
  ∴C_△PMN=PM+PN+MN=P₁M+P₂N+MN=P₁P₂，
  即△PMN周長的最小值為P₁P₂．
  ∵∠AOB=45°，
  ∴∠P₁OP₂=2（∠AOP+∠BOP）=90°．
  ∴△OP₁P₂是等腰直角三角形．
  學以致用：若∠AOB=30°，在∠AOB內部有一點P，分別作點P關于邊OA、OB的對稱點P₁，P₂，順次連接O，P₁，P₂，則△OP₁P₂的形狀是

  三角形．
  （2）【問題探究】如圖2，在△ABC中，AB=AC，∠BAC=30°，點D是BC的中點，若AD=h,請用含有h的代數式表示△ABC的面積．
  （3）【問題解決】如圖3，在四邊形ABCD內有一點P，點P到頂點B的距離為10，∠ABC=60°，點M、N分別是AB、BC邊上的動點，順次連接P、M、N，使△PMN在周長最小的情況下，面積最大，問：是否存在使△PMN在周長最小的條件下，面積最大這種情況？若存在，請求出△PMN的面積的最大值；若不存在，請說明理由．
  組卷：187引用：2難度：0.2

  解析