當前位置：試卷中心 > 試卷詳情

2023-2024學年廣西南寧二中九年級（上）月考數學試卷（10月份）

發布：2024/9/30 6:0:3

一、選擇題（共12小題，每小題3分，共36分，在每小題給出的四個選項中只有一項是符合要求的，）

1．
4
的化簡結果是（　　）
A．2 B．-2 C．±2 D．1
組卷：185引用：3難度：0.7
解析
2．七巧板，又稱七巧圖、智慧板，是中國漢民族的一種古老的傳統智力拼圖游戲，是古代中國勞動人民的發明，如圖所示拼圖是中心對稱圖形的（不考慮拼接線和顏色）是（　　）
A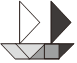． B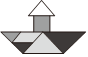． C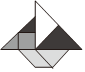． D．
組卷：51引用：1難度：0.8
解析
3．不等式x+3＜5的解集在數軸上表示正確的是（　　）
A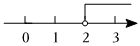． B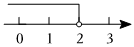． C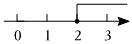． D．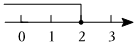
組卷：415引用：6難度：0.7
解析
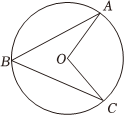4．如圖，在⊙O中，∠AOC=108°，∠ABC的度數是（　　）
A．36° B．45° C．54° D．72°
組卷：143引用：2難度：0.7
解析
5．下列各點在反比例函數
y
=
6
x
圖象上的是（　　）
A．（2，3） B．
（
2
，
1
3
）
C．
（
-
1
，-
1
6
）
D．（6，-1）
組卷：247引用：5難度：0.7
解析
6．陳芋汐在2023年杭州亞運會女子十米跳臺項目中獲得了亞軍，其中第五輪跳水的7個成績分別是（單位：分）：9.5，9.0，9.0，9.0，10.0，9.5，9.0，這組數據的眾數和中位數分別是（　　）
A．9.0；9.5 B．9.0：9.0 C．9.5；9.5 D．9.5；9.25
組卷：372引用：7難度：0.7
解析
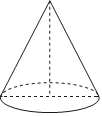7．如圖，小紅要制作一個母線長為7cm,底面圓半徑是6cm的圓錐形小漏斗，若不計損耗，則所需紙板的面積是（　　）
A．36πcm² B．42πcm² C．72πcm² D．84πcm²
組卷：425引用：3難度：0.7
解析
8．如圖所示，是一塊三角形的草坪，現要在草坪上建一涼亭供大家休息，要使涼亭到草坪的三個頂點的距離相等，涼亭的位置應選在（　　）
A．△ABC三邊的垂直平分線的交點
B．△ABC的三條中線的交點
C．△ABC三條角平分線的交點
D．△ABC三條高所在直線的交點
組卷：719引用：28難度：0.9
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本大題共8小題，共72分.解答應寫出文字說明、證明過程或演算步驟.）

25．在《車輪為什么是圓的》課題學習中，小青將車輪設計成半徑為2的正n多邊形，在水平地面上模擬行駛．以n=3為例，如圖1，車輪轉動一次（以一個頂點為支點旋轉），車輪中心的軌跡是BD，點C為中心軌跡最高點（即
?
BD
的中點），轉動一次前后中心的連線是BD（水平線），如圖2，d為點C到BD的距離（即CE的長）．當n取4，5，6時，車輪中心的軌跡分別如圖3、圖4、圖5．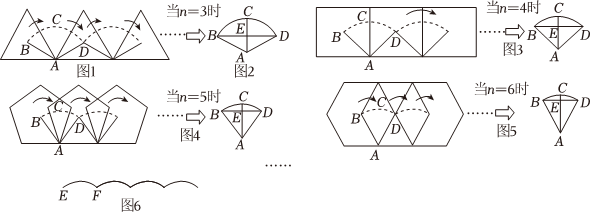

以此類推，當n取不同的值時，分別計算出d的值（結果精確到0.001）．具體數據如下表：

n 3 4 5 6 7 8 9 10 11 ?

d 1.000 0.382 0.268 0.198 0.152 0.121 0.098 0.081 ?

請你協助小青完成以下任務．
（1）求當n=4時，d為何值？（參考數據：
2
≈
1
.
414
）

（2）根據表格數據，d隨n的變化情況為
；當車輪設計成圓形時，d=
，這樣車輛行駛平穩、沒有顛簸感．所以，將車輪設計成圓形．
（3）若路面如圖6形狀，可看成由半徑為2的一些等弧首尾連結而成，若
?
EF
長為
π
9
，為確保車輪平穩滾動，則該車輪應設計成邊數為幾的正多邊形？

組卷：214引用：3難度：0.3

解析

26．如圖，拋物線C₁：y₁=-x²+bx+c 與x軸交于A（1，0），B（-5，0）兩點，與y軸交于點C．
（1）求拋物線y₁的解析式；
（2）若P是拋物線上的任意一點（不與點C重合），假設點P的橫坐標為m,拋物線上點C與點P之間的部分（包含端點）記為圖象G．當m=
3
時，圖象G的最大值與最小值的差為多少？
（3）將線段AB先向左平移1個單位長度，再向上平移5個單位長度，得到線段MN，若拋物線C₂：y₂=-（x+2+n）²+9與線段MN只有一個交點，結合函數圖象，直接寫出n的取值范圍．
?
組卷：147引用：2難度：0.3
解析