2023年福建省莆田市中考數學二檢試卷
發布：2024/4/20 14:35:0
一、選擇題：本大題共10小題，每小題4分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.
-
1．下列四個數中，最大的數是（ ）
組卷：362引用：9難度：0.7 -
2．下列四個幾何體中，主視圖是三角形的是（ ）
組卷：159引用：6難度：0.8 -
3．人工智能是推動全球數字化發展的重要賦能技術．根據中國信通院發布的最新數據測算，預計2023年我國人工智能市場規模達到3043億元．其中304300000000用科學記數法表示為（ ）
組卷：69引用：1難度：0.8 -
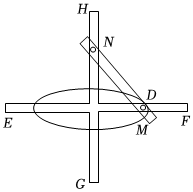4．達芬奇橢圓規是畫橢圓的一種工具，如圖所示，當滑標M在滑槽EF內往復運動，滑標N在滑槽GH內隨之運動，將筆尖放置于D處即可畫出橢圓，則畫出的橢圓是（ ）組卷：74引用：4難度：0.9 -
5．下列各式中，計算結果是a12的是（ ）
組卷：105引用：3難度：0.8 -
6．超市貨架上有一批大小不一的雞蛋，某顧客從中選購了部分大小均勻的雞蛋，設貨架上原有雞蛋的質量（單位：g）平均數和方差分別為
，s2，該顧客選購的雞蛋的質量平均數和方差分別為x，x1，則下列結論一定成立的是（ ）s21組卷：386引用：5難度：0.7 -
7．“曹沖稱象”是流傳很廣的故事，參考他的方法：
第一步先將象牽到大船上，并在船側面標記水位，再將象牽出；
第二步往船上抬入20塊等重的條形石，并在船上留3個搬運工，這時水位恰好到達標記位置：第三步往船上再抬入1塊同樣的條形石，船上只留1個搬運工，發現水位也恰好到達標記位置．
已知搬運工體重均為120斤，設每塊條形石的重量是x斤，根據以上方法可列出的方程是（ ）組卷：218引用：3難度：0.6 -
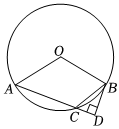8．如圖，在⊙O中，∠AOB=120°，點C在上，連接AC，BC，過點B作BD⊥AC的延長線于點D，當點C從點A運動到點B的過程中，∠CBD的度數（ ）?AB組卷：379引用：5難度：0.5
三、解答題：本大題共9小題，共86分.解答應寫出文字說明、證明過程或演算步驟.
-
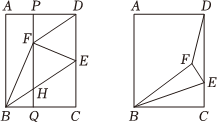24．在矩形ABCD中，點E為線段CD上一動點，將△BCE沿BE折疊得到△BFE，點C的對應點是F，連接DF．
（1）如圖1，BC＞AB，若點E為CD的中點時，過點F作PQ⊥BC于點Q，分別交AD，BE于點P，H．給出下列結論：12
①DF∥EH；
②HF=PF+HQ；
③△EFH為等邊三角形，請任意選擇一個你認為正確的結論加以證明：
（2）如圖2，若BC=3，AB=4．
①在點E運動過程中，當DF取得最小值時，求DE的長；
②設CE=x,tan∠ABF為y,求y關于x的函數關系．組卷：463引用：1難度：0.4 -
25．已知拋物線y=（x+t）2+t+2，其中t是實數．
（1）已知三個點（1，0），（2，0），（2，4），其中有一個點可以是拋物線的頂點，請選出該點并求拋物線的解析式；
（2）在（1）的條件下，點A在拋物線上且其橫坐標為4，過點A作AB⊥x軸于點B．點P為拋物線的頂點，連接PA．點Q為拋物線對稱軸左側上一點，AQ延長線交x軸于點C，QP延長線交AB延長線于點D，連接CD．
①若PA平分∠CAB時，求點Q的坐標；
②設S△PAC=S1，S△BCD=S2，判斷是否為定值？若是，求出該定值；若不是，請說明理由．S1S2組卷：486引用：1難度：0.1