當前位置：試卷中心 > 試卷詳情

2023年安徽省合肥市新站區(qū)中考數學二模試卷

發(fā)布：2024/4/20 14:35:0

一、選擇題（本大題共10小題，每小題4分，共40分）

1．下列各式運算結果是負數的是（　　）
A．（-1）^-2023 B．|-2023| C．
（
-
1
）
2
D．（-2023）⁰
組卷：32引用：2難度：0.6
解析
2．下列計算正確的是（　　）
A．x+x=x² B．（-x）²=-x² C．x⁴÷x²=x² D．x⁴-x²=x²
組卷：37引用：2難度：0.8
解析
3．2023年春節(jié)假日期間，合肥市共接待游客458.6萬人，全市旅游綜合收入27.23億元，其中數據458.6萬用科學記數法可表示為（　　）
A．458.6×10⁴ B．45.86×10⁵ C．4.586×10⁶ D．4.586×10⁷
組卷：27引用：3難度：0.8
解析
4．如圖是一個正方體截去一角后得到的幾何體，它的主視圖是（　　）
A． B． C． D．
組卷：576引用：74難度：0.9
解析
5．一個不等式的解集如圖所示，則這個不等式可以是（　　）
A．x+1＞0 B．x-1＜0 C．2x＞2 D．1-x＜0
組卷：81引用：4難度：0.6
解析
6．如圖，直線m∥n,在等腰△ABC中，AB=AC，∠A=40°，頂點B在直線n上，直線m交AB于點E，交AC于點F，若∠1=α，則∠2的度數是（　　）
A．α-110° B．α-100° C．α-70° D．α-40°
組卷：210引用：2難度：0.7
解析
7．同一元素中質子數相同，中子數不同的各種原子互為同位素，如

12
6
C
與

13
6
C
、

16
8
O
與

17
8
O
．在一次制取CO的實驗中，

12
6
C
與

13
6
C
的原子個數比為2：1，

16
8
O
與

17
8
O
的原子個數比為1：1，若實驗恰好完全反應生成CO，則反應生成

12
6
C
16
8
O
的概率（　　）
A．
1
6
B．
1
3
C．
2
3
D．
1
2
組卷：100引用：3難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

七、（本大題共1小題，每小題12分，共12分）

22．問題背景：如圖1，在等腰△ABC中，AB=AC，AD⊥BC，垂足為點D，在△AEF中，∠AEF=90°，
∠
EAF
=
1
2
∠
BAC
，連接BF，M是BF中點，連接EM和DM，在△AEF繞點A旋轉過程中，線段EM和DM之間存在怎樣的數量關系？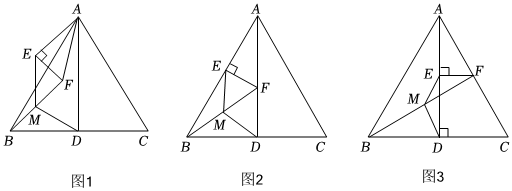

觀察發(fā)現(xiàn)：
（1）為了探究線段EM和DM之間的數量關系，可先將圖形位置特殊化，將△AEF繞點A旋轉，使AE與AB重合，如圖2，易知EM和DM之間的數量關系為
；
操作證明：
（2）繼續(xù)將△AEF繞點A旋轉，使AE與AD重合時，如圖3，（1）中線段EM和DM之間的數量關系仍然成立，請加以證明．
問題解決：
（3）根據上述探究的經驗，我們回到一般情況，如圖1，在其他條件不變的情況下，上述的結論還成立嗎？請說明你的理由．
組卷：219引用：2難度：0.1
解析

八、（本大題共1小題，每小題14分，共14分）

23．如圖，某數學興趣小組以樓梯為場景設計的小球彈射實驗示意圖，樓梯平臺AB寬為3，AB前方有六個臺階T₁～T₆（各拐點均為90°），每個臺階的高為2，寬為2，樓梯平臺到x軸距離OA=14，從y軸上的點C處向右上方彈射出一個小球P（小球視為點），飛行路線為拋物線
L
：
y
=
-
1
2
x
2
+
2
x
+
16
，當點P落到臺階后立即彈起，其飛行路線是與L形狀相同的拋物線．
（1）通過計算判斷小球P第一次會落在哪個臺階上；
（2）若小球P第二次的落點在臺階T₅中點M上，求小球P第二次飛行路線的解析式；
（3）若小球P再次從點M處彈起后落入x軸上一圓柱形小球接收裝置（小球落在圓柱形邊沿也為接收），接收裝置最大截面為矩形EFGH，點E橫坐標為16，EF=1，EH=1，求出小球第三次飛行路線的頂點到x軸距離最小值．
組卷：236引用：2難度：0.4
解析