2022-2023學年廣東省深圳市寶安區西鄉實驗學校八年級（上）月考數學試卷（10月份）

一．選擇題（每題3分，共30分）

• 1．在下列各數

  2

  3

  ，3.1415926，0.

  ??

  213

  ，-

  π

  2

  ，

  3

  ，0.2020020002……（每兩個2之間依次多1個0）中無理數的個數有（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：434引用：8難度：0.6

  解析

• 2．下列各組數不能作為直角三角形三邊長的是（　　）

  A． 3 ， 4 ， 5

  B．3，4，5

  C．5，12，13

  D．8，15，17
  組卷：304引用：3難度：0.6

  解析

• 3．下列各式中，運算正確的是（　　）

  A． 12 = 2 3

  B． 3 3 - 3 = 3

  C． 2 + 3 = 2 3

  D． （ - 2 ） 2 = - 2
  組卷：1181引用：41難度：0.9

  解析

• 4．點P到x軸的距離是3，到y軸的距離是2，且點P在y軸的左側，則點P的坐標是（　　）

  A．（-2，3）或（-2，-3）	B．（-2，3）
  C．（-3，2）或（-3，-2）	D．（-3，2）
  組卷：992引用：5難度：0.8

  解析

• 5．已知點A（-2，y₁）和B（-1，y₂）都在直線y=-3x-1上，則y₁，y₂的大小關系是（　　）

  A．y1＞y2

  B．y1＜y2

  C．y1=y2

  D．大小不確定
  組卷：144引用：4難度：0.6

  解析

• 6．已知一次函數y=kx+3的圖象經過第一、二、四象限，則k的取值范圍是（　　）

  A．k≥0

  B．k＜0

  C．k≥-3

  D．k≤-3
  組卷：1656引用：4難度：0.6

  解析

• 7．下列判斷中，你認為正確的是（　　）

  A．0的倒數是0

  B． π 2 是分數

  C．3＜ 15 ＜4

  D． 9 的值是±3
  組卷：861引用：9難度：0.9

  解析

三．解答題（共55分）

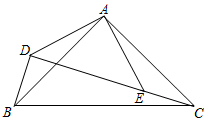• 21．已知：如圖，△ABC和△ADE均為等腰直角三角形，∠BAC=∠DAE=90°，連接AC，BD，且D、E、C三點在一直線上，AD=

  2

  ，DE=2EC．
  （1）求證：△ADB≌△AEC；
  （2）求線段BC的長．
  組卷：964引用：3難度：0.5

  解析

• 22．【問題背景】
  學校數學興趣小組在專題學習中遇到一個幾何問題：如圖1，已知等邊△ABC，D是△ABC外一點，連接AD、CD、BD，若∠ADC=30°，AD=3，BD=5，求CD的長．
  該小組在研究如圖2中△OMN≌△OPQ中得到啟示，于是作出圖3，從而獲得了以下的解題思路，請你幫忙完善解題過程．
  解：如圖3所示，以DC為邊作等邊△CDE，連接AE．
  ∵△ABC、△DCE是等邊三角形，
  ∴BC=AC，DC=EC，∠BCA=∠DCE=60°．
  ∴∠BCA+∠ACD=

  +∠ACD，
  ∴∠BCD=∠ACE，
  ∴

  ，
  ∴AE=BD=5．
  ∵∠ADC=30°，∠CDE=60°，
  ∴∠ADE=∠ADC+∠CDE=90°．
  ∵AD=3，
  ∴CD=DE=

  ．
  【嘗試應用】
  如圖4，在△ABC中，∠ABC=45°，AB=

  2

  ，BC=4，以AC為直角邊，A為直角頂點作等腰直角△ACD，求BD的長．
  【拓展創新】
  如圖5，在△ABC中，AB=4，AC=8，以BC為邊向外作等腰△BCD，BD=CD，∠BDC=120°，連接AD，求AD的最大值．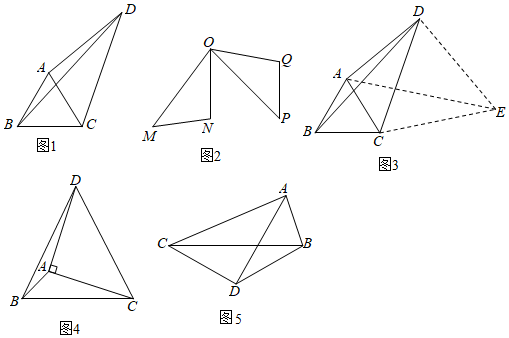
  
  組卷：2615引用：3難度：0.3

  解析