2023年陜西省榆林市神木市店塔初級中學中考數學模擬試卷

一、選擇題（共8小題，每小題3分，計24分．每小題只有一個選項是符合題目要求的）

• 1．計算（-7）+3的結果是（　　）

  A．-4

  B．-10

  C．-21

  D．4
  組卷：761引用：5難度：0.8

  解析

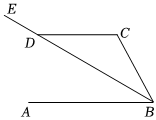• 2．如圖，已知AB∥CD，BE平分∠ABC，且交CD于點D，∠CDE=140°，則∠C的度數是（　　）

  A．50°

  B．70°

  C．100°

  D．140°
  組卷：138引用：3難度：0.7

  解析

• 3．若實數a、b在數軸上的位置如圖所示，則下列結論中正確的是（　　）

  A．-a＞-b

  B．|a|＜|b|

  C．ab＞0

  D．a＜0＜b
  組卷：57引用：2難度：0.7

  解析

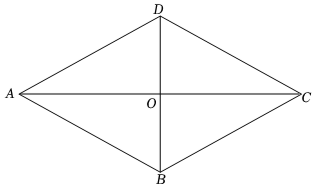• 4．如圖，在菱形ABCD中，對角線AC，BD相交于點O，下列結論中錯誤的是（　　）

  A．AB=AD

  B．AC⊥BD

  C．AC=BD

  D．∠DAC=∠BAC
  組卷：1570引用：16難度：0.8

  解析

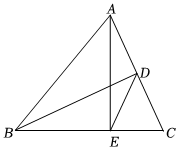• 5．如圖，在△ABC中，AB=CB=13，BD⊥AC于點D且BD=12，AE⊥BC于點E，連接DE，則DE的長為（　　）

  A． 5 2

  B． 7 2

  C．5

  D．6
  組卷：696引用：8難度：0.7

  解析

• 6．若一次函數y=（m-3）x-2的圖象經過第二、三、四象限，則常數m的取值范圍是（　　）

  A．m＜3

  B．m＜0

  C．m＞3

  D．m＞2
  組卷：615引用：2難度：0.7

  解析

• 7．如圖，△ABC的頂點A，B，C均在⊙O上，若∠ABC=37°，則∠OAC的大小是（　　）

  A．74°

  B．63°

  C．53°

  D．43°
  組卷：100引用：2難度：0.6

  解析

• 8．已知二次函數y=ax²-2ax+1（a為常數）的圖象與x軸交于兩點（x₁，0）和（x₂，0）且x₁＜0＜x₂．若此拋物線上有三點A（-2，y₁），B（1，y₂），C（3，y₃），則y₁，y₂，y₃的大小關系是（　　）

  A．y1＞y2＞y3

  B．y1＞y3＞y2

  C．y2＞y1＞y3

  D．y2＞y3＞y1
  組卷：407引用：4難度：0.6

  解析

三、解答題（共13小題，計81分．解答應寫出過程）

• 25．高爾夫是一種將享受大自然樂趣、體育鍛煉和游戲集于一身的運動．如圖，方方在一次高爾夫球爭霸賽中，從山坡下O點打出一桿，球向球洞A點飛去，且路線為拋物線．如果不考慮空氣阻力，當球移動的水平距離為9米時，球達到最大高度12米．以點O為原點建立平面直角坐標系，則拋物線的頂點為點B，球洞A點的坐標為（12，4

  3

  ）．
  （1）求出球的飛行路線所在拋物線的函數表達式；
  （2）判斷方方這一桿能否把高爾夫球從O點直接打人球洞A點，并說明理由．
  組卷：270引用：2難度：0.5

  解析

• 26．問題提出
  （1）如圖①，在四邊形ABCD中，∠BAE=∠CDE=90°，點E在線段AD上，連接BE，CE，BC，使得∠BEC=90°，若BE=CE，則圖中與AE相等的線段是

  ；
  問題探究
  （2）如圖②，在△ABC中，點D是BC上一點，∠CAD=90°，AC=AD，∠DBA=∠DAB，AB=2

  2

  ，求點C到邊AB的距離；
  問題解決
  （3）如圖③，有一塊矩形ABCD板材，AB=10dm,AD=9dm,李師傅因制作一模型需要一個形狀特殊且面積為61dm²的四邊形EFGC，已知點E在BC邊上，BE=1dm,現在還需要在邊AB，AD上確定點F，點G，使得FG⊥CG，且GC=2FG．李師傅通過測量采用了如下操作：分別在AB和AD上測量2dm和5dm的長度，確定為點F，點G，連接EF、FG和CG請問，按照李師傅的作法，裁得的四邊形EFGC是否符合要求？請證明你的結論．
  
  組卷：188引用：3難度：0.2

  解析