2022-2023學年山東省濟寧市汶上一中高二（上）第一次月考數學試卷

一、單選題（本大題共8小題，共40.0分．在每小題列出的選項中，選出符合題目的一項）

• 1．在空間四邊形OABC中，

  OA

  +

  AB

  -

  CB

  等于（　　）

  A． OA

  B． AB

  C． OC

  D． AC
  組卷：1002引用：34難度：0.9

  解析

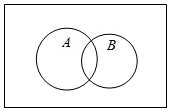• 2．已知一個古典概型的樣本空間Ω和事件A，B如圖所示．其中n（Ω）=12，n（A）=6，n（B）=4，n（A∪B）=8，則事件A與事件

  B

  （　　）

  A．是互斥事件，不是獨立事件

  B．不是互斥事件，是獨立事件

  C．既是互斥事件，也是獨立事件

  D．既不是互斥事件，也不是獨立事件
  組卷：1006引用：7難度：0.9

  解析

• 3．若

  a

  ，

  b

  ，

  c

  是空間任意三個向量，λ∈R，下列關系式中，不成立的是（　　）

  A． a + b = b + a	B． λ （ a + b ） = λ a + λ b
  C． （ a + b ） + c = a + （ b + c ）	D． b = λ a
  組卷：199引用：5難度：0.9

  解析

• 4．在一次隨機試驗中，已知A，B，C三個事件發生的概率分別為0.2，0.3，0.5，則下列說法一定正確的是（　　）

  A．B與C是互斥事件	B．A+B與C是對立事件
  C．A+B+C是必然事件	D．0.3≤P（A+B）≤0.5
  組卷：296引用：5難度：0.8

  解析

• 5．若在同等條件下進行n次重復試驗得到某個事件A發生的頻率f（n），則隨著n的逐漸增加，有（　　）

  A．f（n）與某個常數相等

  B．f（n）與某個常數的差逐漸減小

  C．f（n）與某個常數差的絕對值逐漸減小

  D．f（n）在某個常數附近擺動并趨于穩定
  組卷：99引用：11難度：0.7

  解析

• 6．某射擊運動員射擊一次命中目標的概率為p,已知他獨立地連續射擊三次，至少有一次命中的概率

  37

  64

  ，則p為（　　）

  A． 1 4

  B． 3 4

  C． 3 3 8

  D． 37 8
  組卷：638引用：9難度：0.8

  解析

• 7．給出下列命題：
  ①若A，B，C，D是空間任意四點，則有

  AB

  +

  BC

  +

  CD

  +

  DA

  =

  0

  ；
  ②

  |

  a

  |

  -

  |

  b

  |

  =

  |

  a

  +

  b

  |

  是

  a

  ，

  b

  共線的充要條件；
  ③若

  AB

  ，

  CD

  共線，則AB∥CD；
  ④對空間任意一點O與不共線的三點A，B，C，若

  OP

  =

  x

  OA

  +

  y

  OB

  +

  z

  OC

  （其中x,y,z∈R），則P，A，B，C四點共面．
  其中不正確命題的個數是（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：185引用：4難度：0.7

  解析

四、解答題（本大題共6小題，17題10分其他題目各12分共70.0分．解答應寫出文字說明，證明過程或演算步驟）

• 21．某項選拔共有四輪考核．每輪設有一個問題，能正確回答問題者進入下一輪考核，否則即被淘汰．已知某選手能正確回答第一、二、三、四輪的問題的概率分別為

  4

  5

  、

  3

  5

  、

  2

  5

  、

  1

  5

  ，且各輪問題能否正確回答互不影響．
  （Ⅰ）求該選手進入第四輪才被淘汰的概率；
  （Ⅱ）求該選手至多進入第三輪考核的概率．
  （注：本小題結果可用分數表示）
  組卷：521引用：15難度：0.5

  解析

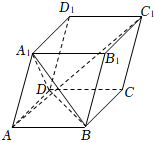• 22．已知平行六面體ABCD-A₁B₁C₁D₁的所有棱長均為1，∠BAD=∠BAA₁=∠DAA₁=60°．用向量解決下面的問題
  （1）求AC₁的長；
  （2）求證：AC₁⊥平面A₁BD．
  組卷：60引用：1難度：0.6

  解析