當前位置：試卷中心 > 試卷詳情

2023-2024學年浙江省寧波市北侖中學高二（上）期初數學試卷

發布：2024/8/5 8:0:8

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．已知
z
=
2
+
i
1
+
i
2
+
i
5
，則z的虛部是（　　）
A．-2i B．2i C．-2 D．2
組卷：35引用：3難度：0.8
解析
2．設等比數列{a_n}的首項為1，公比為q,前n項和為S_n．令b_n=S_n+2，若{b_n}也是等比數列，則q=（　　）
A．
1
2
B．
3
2
C．
5
2
D．
7
2
組卷：2717引用：2難度：0.8
解析
3．下列正方體中，A，B為正方體的兩個頂點，M，N，P分別為其所在棱的中點，則能滿足AB∥平面MNP的是（　　）
A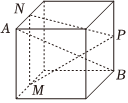． B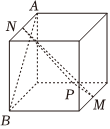． C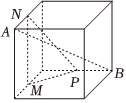． D．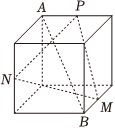

組卷：206引用：4難度：0.5
解析
4．已知一個等比數列的前n項和、前2n項和、前3n項和分別為P、Q、R，則下列等式正確的是（　　）
A．P+Q=R B．Q²=PR
C．（P+Q）-R=Q² D．P²+Q²=P（Q+R）
組卷：274引用：4難度：0.5
解析
5．在銳角△ABC中，角A，B，C的對邊分別為a,b,c,若a²=2S+（b-c）²，其中S為△ABC的面積，則sinB的取值范圍為（　　）
A．
（
0
，
3
5
）
B．
（
0
，
4
5
）
C．
（
3
5
，
1
）
D．
（
4
5
，
1
）
組卷：115引用：3難度：0.6
解析
6．三棱錐P-ABC中，平面PAB⊥平面ABC，△ABC是邊長為2的正三角形，
PA
=
PB
=
3
，則三棱錐P-ABC外接球的表面積為（　　）
A．
35
π
3
B．
35
π
6
C．
35
π
12
D．
35
π
24
組卷：450引用：6難度：0.5
解析
7．若O是△ABC的外心，且
AC
2
AB
2
?
（
AB
?
AO
）
+
AB
2
AC
2
?
（
AC
?
AO
）
=
5
2
AO
2
，則sinB+2sinC的最大值是（　　）
A．
3
+
2
2
B．
3
2
+
2
C．
5
2
D．2
2
組卷：532引用：3難度：0.3
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

21．如圖，在平行四邊形ABCD中，∠ABC=60°，AD=2AB=4，E為AD的中點，以EC為折痕將△CDE折起，使點D到達點P的位置，且PB=
10
，F，G分別為BC，PE的中點．
（1）證明：PB∥平面AFG；
（2）若平面PAB與平面PEF的交線為l,求直線l與平面PBC所成角的正弦值．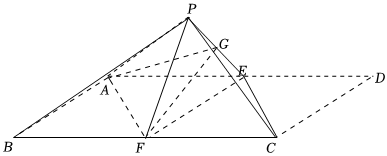
組卷：306引用：5難度：0.3
解析
22．已知數列{a_n}中a₁=1，關于x的函數f（x）=x²-na_n+1cosx+（n+1）a_n有唯一零點，記
S
n
=
1
a
n
2
+
1
a
n
2
+
1
+
1
a
n
2
+
2
+
…
+
1
（
a
n
+
1
）
2
-
1
．
（Ⅰ）判斷函數f（x）=x²-na_n+1cosx+（n+1）a_n的奇偶性并證明；
（Ⅱ）求a_n；
（Ⅲ）求證：
2
n
+
1
＜
S
n
．
組卷：40引用：1難度：0.4
解析