2021-2022學年湖南省永州市黃岡博才學校九年級（下）第一次月考數學試卷

一、選擇題（40=4×10）

• 1．下列函數中一定是二次函數的是（　　）

  A．y=（x+3）2-x2	B．y=x2- 1 x
  C．y=ax2+bx+c	D．y=（2x-1）（x+2）
  組卷：184引用：3難度：0.9

  解析

• 2．有下列說法：①直徑是圓中最長的弦；②等弧所對的弦相等；③圓中90°的角所對的弦是直徑；④相等的圓心角所對的弧長相等；⑤一條弦平分另一條弦，則垂直于這條弦．其中正確的是（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：234引用：2難度：0.6

  解析

• 3．若A（-5，y₁），B（-3，y₂），C（0，y₃）為二次函數y=x²+4x-5的圖象上的三點，則y₁、y₂、y₃的大小關系是（　　）

  A．y2＜y3＜y1

  B．y1＜y2＜y3

  C．y3＜y1＜y2

  D．y1＜y3＜y2
  組卷：425引用：8難度：0.7

  解析

• 4．如圖，等邊三角形ABC和正方形ADEF都內接于⊙O，則∠BED（　　）

  A．45°

  B．30°

  C．20°

  D．15°
  組卷：156引用：4難度：0.6

  解析

• 5．一扇形的半徑為24cm,若此扇形圍成的圓錐的底面半徑為10cm,那么這個扇形的面積是（　　）

  A．120πcm 2

  B．240πcm 2

  C．260πcm 2

  D．480πcm 2
  組卷：21引用：2難度：0.7

  解析

• 6．如圖是由若干小正方體組成的幾何體的俯視圖，小正方形中的數字表示該位置小正方體的個數，這個幾何體的主視圖是（　　）

  A．

  B．

  C．

  D．
  組卷：681引用：10難度：0.7

  解析

• 7．如圖，⊙A過原點O，分別與x軸、y軸交于點C和點D，點B在⊙A上，已知∠B=30°，⊙A的半徑為2，則圓心A的坐標是（　　）

  A．（ 3 ，1）

  B．（1， 3 ）

  C．（ 2 ，1）

  D．（1， 2 ）
  組卷：523引用：2難度：0.6

  解析

• 8．某農場擬建一間矩形種牛飼養室，飼養室的一面靠現有墻（墻足夠長），并在如圖所示位置留2m寬的門，已知計劃中的建筑材料可建圍墻（不包括門）的總長度為50m.設飼養室長為xm,占地面積為ym²，則y關于x的函數表達式是（　　）

  A．y=-x2+50x	B．y=- 1 2 x2+24x
  C．y=- 1 2 x2+25x	D．y=- 1 2 x2+26x
  組卷：2425引用：11難度：0.7

  解析

三、解答題（共78分）

• 25．【閱讀材料】如圖1所示，對于平面內⊙P，在⊙P上有弦AB，取弦AB的中點M，我們把弦AB的中點M到某點或某直線的距離叫做弦AB到這點或者這條直線的“密距”．例如：圖1中線段MO的長度即為弦AB到原點O的“密距”．過點M作y軸的垂線交y軸于點N，線段MN的長度即為弦AB到y軸的“密距”．
  【類比應用】
  已知⊙P的圓心為P（0，4），半徑為2，弦AB的長度為2，弦AB的中點為M．
  （1）當AB∥y軸時，如圖2所示，圓心P到弦AB的中點M的距離是

  ，此時弦AB到原點O的“密距”是

  ．
  （2）①如果弦AB在⊙P上運動，在運動過程中，圓心P到弦AB的中點M的距離變化嗎？若不變化，請求出PM的長，若變化，請說明理由．
  ②直接寫出弦AB到原點的“密距”d的取值范圍

  ；
  【拓展應用】如圖3所示，已知⊙P的圓心為P（0，4），半徑為2，點A（0，2），點B為P上的一動點，有直線y=-x-3，弦AB到直線y=-x-3的“密距”的最大值是

  （直接寫出答案）．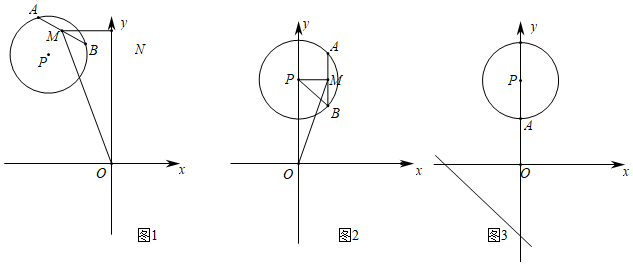
  
  組卷：258引用：2難度：0.2

  解析

• 26．如圖，拋物線y=ax²+bx+c（a≠0）與x軸交于A、B兩點，與y軸交于點C（0，3），且OB=OC=3OA，直線y=x+1與拋物線交于A、D兩點，與y軸交于點E，點Q是拋物線的頂點，設直線AD上方拋物線上的動點P的橫坐標為m.
  
  （1）求該拋物線的解析式及頂點Q的坐標；
  （2）連接PA、PD，當m為何值時，

  S

  △

  PAD

  =

  1

  2

  S

  △

  DAB

  ；
  （3）在直線AD上是否存在一點H使△PQH為等腰直角三角形，若存在請直接寫出點P的坐標，不存在請說明理由．
  組卷：67引用：4難度：0.1

  解析