2022-2023學年山西省陽泉市高新區九年級(上)期末數學試卷
發布:2024/9/10 0:0:8
一、選擇題(本大題共10個小題,每小題3分,共30分.在每小題所給出的四個選項中,只有一項符合題目要求,請選出并在答題卡上將該項涂黑)
-
1.已知△ABC中,∠ACB=90°,AC=2,BC=1,則tanA的值為( )
A. 12B. 55C. 255D.2 組卷:390引用:2難度:0.7 -
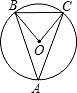 2.如圖,△ABC內接于⊙O,∠A=40°,則∠BOC的度數為( )
2.如圖,△ABC內接于⊙O,∠A=40°,則∠BOC的度數為( )A.20° B.40° C.60° D.80° 組卷:194引用:36難度:0.9 -
3.已知y是x的反比例函數,下表給出了x與y的一些值,則表中“▲”處的數為( )
x -6 -2 5 y 1 3 ▲ A.-2 B.-1.2 C.1.2 D.2 組卷:154引用:4難度:0.5 -
4.將二次函數y=(x+3)2-10的圖象先向右平移2個單位長度,再向上平移8個單位長度,得到的拋物線的解析式是( )
A.y=(x+5)2-2 B.y=(x-1)2+2 C.y=(x+1)2-2 D.y=(x-5)2+2 組卷:578引用:5難度:0.6 -
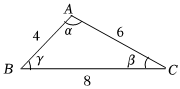 5.如圖是老師畫出的△ABC,已標出三邊的長度.下面四位同學畫出的三角形與老師畫出的△ABC不一定相似的是( )
5.如圖是老師畫出的△ABC,已標出三邊的長度.下面四位同學畫出的三角形與老師畫出的△ABC不一定相似的是( )A. 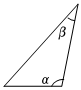
B. 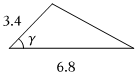
C. 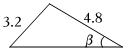
D. 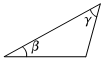 組卷:938引用:15難度:0.6
組卷:938引用:15難度:0.6 -
6.學校藝術節上,同學們繪制了非常美麗的畫并且在其周圍裱上等寬的邊框做成藝術墻.下面是王亮從藝術墻上選取的四幅形狀不同的作品,在同一幅作品中,內、外邊框的圖形不一定相似的是( )
A. 
B. 
C. 
D.  組卷:274引用:9難度:0.6
組卷:274引用:9難度:0.6 -
 7.公元前3世紀,古希臘科學家阿基米德發現:若兩物體與支點的距離與其重量成反比,則杠桿平衡.后來人們把它歸納為“杠桿原理”.通俗地說,杠桿原理為:阻力×阻力臂=動力×動力臂.小偉欲用撬棍撬動一塊大石頭,已知阻力和阻力臂分別為1200N和0.5m,動力臂為1.5m,則撬動這塊大石頭至少需要的動力是( )
7.公元前3世紀,古希臘科學家阿基米德發現:若兩物體與支點的距離與其重量成反比,則杠桿平衡.后來人們把它歸納為“杠桿原理”.通俗地說,杠桿原理為:阻力×阻力臂=動力×動力臂.小偉欲用撬棍撬動一塊大石頭,已知阻力和阻力臂分別為1200N和0.5m,動力臂為1.5m,則撬動這塊大石頭至少需要的動力是( )A.360N B.400N C.450N D.600N 組卷:156引用:3難度:0.6 -
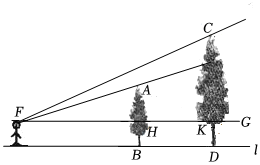 8.如圖,左、右并排的兩棵大樹的高分別為AB=8m,CD=12m,兩樹底部的距離BD=5m,王紅估計自己眼睛距地面1.6m.她沿著連接這兩棵樹的一條水平直路l從左向右前進,在前進的過程中,她發現看不到右邊較高的樹的頂端C,此時,她與左邊較低的樹AB的水平距離( )
8.如圖,左、右并排的兩棵大樹的高分別為AB=8m,CD=12m,兩樹底部的距離BD=5m,王紅估計自己眼睛距地面1.6m.她沿著連接這兩棵樹的一條水平直路l從左向右前進,在前進的過程中,她發現看不到右邊較高的樹的頂端C,此時,她與左邊較低的樹AB的水平距離( )A.小于8m B.小于9m C.大于8m D.大于9m 組卷:890引用:3難度:0.5
三、解答題(本大題共8個小題,共75分.解答時應寫出必要的文字說明、證明過程或演算步驟)
-
23.綜合與探究
問題情境:
如圖,已知AB為⊙O的直徑,點C為⊙O上異于A,B的一點,過點C作⊙O的切線CE,過點A作AD⊥CE于點D,連接OC.
探究發現:
(1)證明:無論點C在何處,將△ADC沿AC折疊,點D一定落在直徑AB上;
探究引申:
(2)如圖2,勤奮小組繼續探究發現,若△AOC是等腰三角形且對稱軸經過點D,此時,CD與AB存在數量關系,請寫出結論并證明;
探究規律:
(3)如圖3,智慧小組在勤奮小組的啟發下發現當△AOC為正三角形時,CD與AB存在的數量關系是:CD=AB.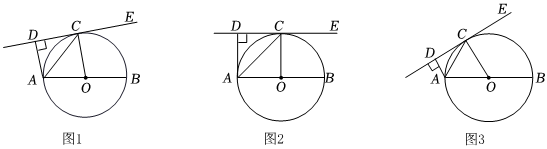 組卷:409引用:3難度:0.5
組卷:409引用:3難度:0.5 -
24.綜合與實踐
如圖,拋物線y=ax2+x+c與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C,點B的坐標是(4,0),點C的坐標是(0,2),拋物線的對稱軸交x軸于點D,連接CD.32
(1)求拋物線的解析式;
(2)在拋物線的對稱軸上是否存在點P,使△PCD是以CD為腰的等腰三角形?如果存在,求出點P的坐標;如果不存在,請說明理由;
(3)點E在x軸上運動,點F在拋物線上運動,當以點B,C,E,F為頂點的四邊形是平行四邊形,直接寫出點E的坐標.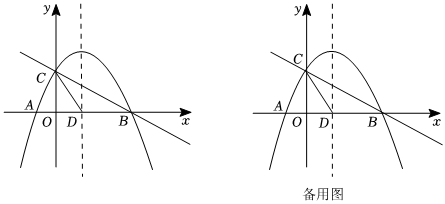 組卷:957引用:5難度:0.4
組卷:957引用:5難度:0.4


