2021-2022學年山西省太原外國語學校九年級（上）月考數學試卷（12月份）

一．選擇題（共10小題）

• 1．下列關系式中，表示y是x的反比例函數的是（　　）

  A． y = 1 x 2

  B． y = x 3

  C． y = 2 x + 1

  D． y = 3 x
  組卷：57引用：3難度：0.6

  解析

• 2．如圖所示的禮品盒的主視圖是（　　）

  A．

  B．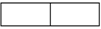

  C．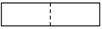

  D．
  組卷：4引用：1難度：0.8

  解析

• 3．已知△ABC∽△DEF，相似比為1：2，且△DEF的面積為12，則△ABC的面積為（　　）

  A．48

  B．12

  C．6

  D．3
  組卷：16引用：1難度：0.5

  解析

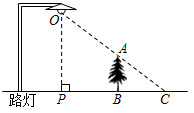• 4．如圖，小樹AB在路燈O的照射下形成投影BC．若樹高AB=2m,樹影BC=3m,樹與路燈的水平距離BP=4.5m.則路燈的高度OP為（　　）

  A．3m

  B．4m

  C．4.5m

  D．5m
  組卷：2259引用：27難度：0.5

  解析

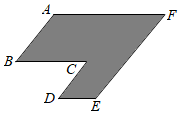• 5．如圖，陰影部分是一個菱形剪去一個平行四邊形后所剩下的，要想知道陰影部分的周長，需要測量線段（　　）的長度．

  A．AB與BC

  B．AB與DE

  C．AF

  D．AB
  組卷：241引用：5難度：0.7

  解析

• 6．數學興趣小組在一次用頻率估計概率的實驗中統計了某一結果出現的頻率，繪制了如圖所示的頻率分布散點圖，則符合這一結果的實驗可能是（　　）
  

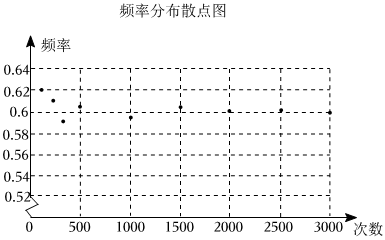
  A．拋擲一枚硬幣，正面向上的概率

  B．拋擲一枚骰子，朝上一面的點數為3的倍數的概率

  C．從裝有3個紅球、2個黃球袋子中，隨機摸出一球為紅球的概率

  D．一副去掉大小王的普通撲克牌洗勻后，從中任抽一張，牌的花色是紅桃的概率
  組卷：68引用：2難度：0.7

  解析

• 7．《九章算術》是我國古代數學的經典著作，它的出現標志著中國古代數學形成了完整的體系，其“勾股”章中記載了一個數學問題：“今有戶高多于廣六尺，兩隅相去適一丈，問戶高、廣各幾何？”譯文為：“已知有一扇矩形門的高比寬多6尺，門的對角線長為1丈（1丈=10尺），那么門的高和寬各是多少？”如果設門的寬為x尺，則可列方程為（　　）

  A．x2+（x+6）2=102	B．x2+（x+6）2=12
  C．x2+（x-6）2=102	D．x2+（x-6）2=12
  組卷：445引用：14難度：0.6

  解析

• 8．如圖，矩形ABCD的對角線AC、BD相交于點O，過點O的直線EF分別交AD、BC于點E、F．若AB=6，BC=10則圖中陰影部分的面積為（　　）

  A．24

  B．30

  C．48

  D．60
  組卷：13引用：2難度：0.5

  解析

三、解答題（本大題共8個小題，共75分）

• 23．感知：
  （1）數學課上，老師給出了一個模型：如圖1，∠BAD=∠ACB=∠AED=90°，由∠1+∠2+∠BAD=180°，∠2+∠D+∠AED=180°，可得∠1=∠D；又因為∠ACB=∠AED=90°，可得△ABC∽△DAE，進而得到

  BC

  AC

  =

  ．我們把這個數學模型稱為“一線三等角”模型．
  應用：
  （2）實戰組受此模型的啟發，將三等角變為非直角，如圖2，在△ABC中，點D在邊BC上，并且DA=DE，∠B=∠ADE=∠C．若BC=a,AB=b,求CE的長度（用含a,b的代數式表示）．
  拓展：
  （3）創新組突發奇想，將此模型遷移到平行四邊形中，如圖3，在?ABCD中，E為邊BC上的一點，F為邊AB上的一點．若∠DEF=∠B．求證：AB?FE=BE?DE．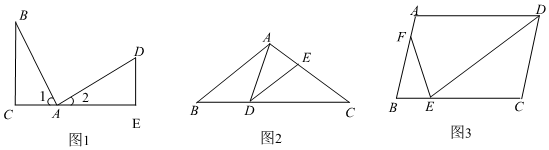
  
  組卷：771引用：4難度：0.2

  解析

• 24．綜合與探究
  如圖，直線y=-x+m與反比例函數

  y

  =

  k

  x

  的圖象相交于點A（-2，n），與x軸交于點B（2，0）．
  （1）求m和k的值；
  （2）點C在x軸的負半軸上，直線AC與反比例函數

  y

  =

  k

  x

  的圖象交于點D，若D是AC的中點，求△AOC的面積；
  （3）若點P與點O關于直線AB對稱，連接AP．
  ①求點P的坐標；
  ②若點M在反比例函數

  y

  =

  k

  x

  的圖象上，點N在x軸上，以點A，P，M，N為頂點的四邊形能否為平行四邊形？若能，直接寫出點M的坐標；若不能，請說明理由．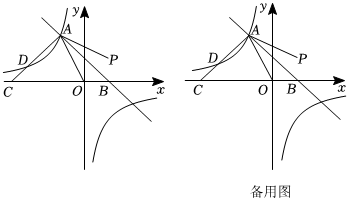
  
  組卷：85引用：1難度：0.1

  解析