當前位置：試卷中心 > 試卷詳情

2022-2023學年山東省日照市東港區日照港中學八年級（下）段測數學試卷（一）

發布：2024/12/9 5:0:1

一、選擇題。（本大題共12小題，共36分。在每小題列出的選項中，選出符合題目的一項）

1．下列二次根式中能與2
3
合并的是（　　）
A．
8
B．
1
3
C．
18
D．
9
組卷：4318引用：55難度：0.9
解析
2．下列運算正確的是（　　）
A．2+
3
=2
3
B．5
2
-
2
=5 C．5
2
a
+
2
a
=6
2
a
D．
y
+2
x
=3
xy
組卷：443引用：6難度：0.7
解析
3．以下列各組數的長為邊作三角形，不能構成直角三角形的是（　　）
A．3，4，5 B．4，5，6 C．6，8，10 D．9，12，15
組卷：182引用：9難度：0.7
解析
4．把代數式（a-1）
1
1
-
a
中的a-1移到根號內，那么這個代數式等于（　　）
A．-
1
-
a
B．
a
-
1
C．
1
-
a
D．-
a
-
1
組卷：2600引用：8難度：0.7
解析
5．如圖，“趙爽弦圖”是由四個全等的直角三角形與中間的一個小正方形拼成的大正方形．若圖中的直角三角形的兩條直角邊的長分別為1和3，則中間小正方形的周長是（　　）
A．4 B．8 C．12 D．16
組卷：943引用：10難度：0.7
解析
6．當a=
5
+2，b=
5
-2時，a²+ab+b²的值是（　　）
A．10 B．15 C．18 D．19
組卷：351引用：2難度：0.8
解析
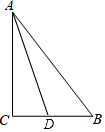7．如圖，△ABC中，AC=6，BC=8，AB=10．AD為△ABC的角平分線，CD的長度為（　　）
A．2 B．
5
2
C．3 D．
10
3
組卷：408引用：3難度：0.7
解析
8．如圖所示，ABCD是長方形地面，長AB=20，寬AD=10，中間整有一堵磚墻高MN=2，一只螞蟻從A點爬到C點，它必須翻過中間那堵墻，則它至少要走（　　）
A．20 B．24 C．25 D．26
組卷：1430引用：8難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題。（本大題共6小題，共52.0分。解答應寫出文字說明，證明過程或演算步驟）

24．閱讀材料：我們已經知道，形如
c
a
±
b
的無理數的化簡要借助平方差公式：
例如：
3
2
-
3
=
3
×
（
2
+
3
）
（
2
-
3
）
（
2
+
3
）
=
6
+
3
3
2
2
-
（
3
）
2
=
6
+
3
3
4
-
3
=
6
+
3
3
．下面我們來看看完全平方公式在無理數化簡中的作用．
問題提出：
7
+
4
3
該如何化簡？
建立模型：形如
m
+
2
n
的化簡，只要我們找到兩個數a,b,使a+b=m,ab=n,這樣
（
a
）
2
+
（
b
）
2
=m,
a
?
b
=
n
，
那么便有：
m
±
2
n
=
（
a
±
b
）
2
=
a
±
b
（a＞b），
問題解決：化簡：
7
+
4
3
，
解：首先把
7
+
4
3
化為
7
+
2
12
，這里m=7，n=12，由于4+3=7，4×3=12，即
（
4
）
2
+
（
3
）
2
=7，
4
×
3
=
12

∴
7
+
4
3
=
7
+
2
12
=
（
4
+
3
）
2
=
2
+
3
．
模型應用1：利用上述解決問題的方法化簡下列各式：
（1）
6
+
2
5
；
（2）
13
-
4
10
；
模型應用2：
（3）在Rt△ABC中，∠C=90°，AB=4-
3
，AC=
3
，那么BC邊的長為多少？（結果化成最簡）．
組卷：1901引用：4難度：0.4
解析
25．如圖1是著名的趙爽弦圖，由四個全等的直角三角形拼成，用它可以證明勾股定理，思路是：大正方形的面積有兩種求法，一種是等于c²，另一種是等于四個直角三角形與一個小正方形的面積之和，即
1
2
ab
×
4
+
（
b
-
a
）
2
，從而得到等式c²=
1
2
ab
×
4
+
（
b
-
a
）
2
，化簡便得結論a²+b²=c²．這里用兩種求法來表示同一個量從而得到等式或方程的方法，我們稱之為“雙求法”．現在，請你用“雙求法”解決下面兩個問題
（1）如圖2，在Rt△ABC中，∠ACB=90°，CD是AB邊上的高，AC=3，BC=4，求CD的長度．
（2）如圖3，在△ABC中，AD是BC邊上的高，AB=4，AC=5，BC=6，設BD=x,求x的值．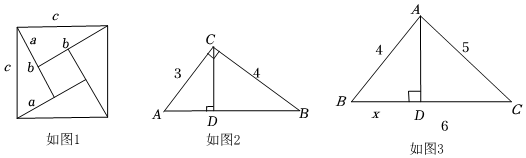
組卷：1805引用：11難度：0.5
解析