2023-2024學年遼寧省鞍山市立山區九年級（上）期中數學試卷
發布：2024/10/18 17:0:4
一、選擇題（每小題3分，共30分）
-
1．下列有關環保的四個圖形中，既是軸對稱圖形，又是中心對稱圖形的是（ ）
組卷：128引用：4難度：0.9 -
2．一元二次方程x2+2x-5=0的根的情況是（ ）
組卷：354引用：6難度：0.8 -
3．如圖，在直角坐標系中，矩形OABC的頂點O在坐標原點，邊OA在x軸上，OC在y軸上，如果矩形OA′B′C′與矩形OABC關于點O位似，且矩形OA′B′C′的面積等于矩形OABC面積的，那么點B′的坐標是（ ）14組卷：931引用：24難度：0.7 -
4．要將拋物線y=x2平移后得到拋物線y=x2+4x+5，下列平移方法正確的是（ ）
組卷：1715引用：8難度：0.8 -
5．如圖，在Rt△ABC中，∠ACB=90°，∠A=60°，AC=2，將△ABC繞點C按逆時針方向旋轉得到△A'B'C，此時點A'恰好在AB邊上，則點B'與點B之間的距離為（ ）組卷：256引用：7難度：0.5 -
6．若將方程x2-6x-5=0化成（x+a）2=b（a,b為常數）的形式，則a+b的值是（ ）
組卷：352引用：6難度：0.6 -
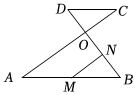7．如圖，AC，BD相交于點O，AB∥DC，M是AB的中點，MN∥AC，交BD于點N，若DO：OB=1：2，AC=12，則MN的長為（ ）組卷：2623引用：17難度：0.7
三、解答題：
-
22．發現問題：
如圖1，在筆記本的橫線上取一點O，以O為圓心，相鄰橫線的間距為半徑畫圓，然后半徑依次增加一個間距繼續畫同心圓，愛思考的小杰同學發現同心圓與每條橫線的2個交點的位置隨著半徑的改變而改變．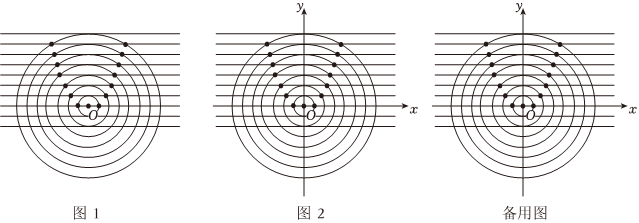
?
提出問題：
探究這些點的縱坐標與橫坐標之間的關系．
分析問題：
小杰利用已學知識和經驗，以圓心O為原點，過點O的橫線所在直線為x軸，過點O且垂直于橫線的直線為y軸，相鄰橫線的間距為一個單位長度，建立平面直角坐標系，如圖2所示，小杰利用圖2坐標系，通過計算得到一些數據：
請直接寫出圓的半徑為5時的交點坐標 ；半徑 1 2 3 4 5 … 交點坐標 （-1，0），
（1，0）（ ，1），3
（-，1）3（ ，2），5
（-，2）5（ ，3），7
（-，3）7…
解決問題：
（1）請你根據小杰的思路，計算圓半徑為n時的交點坐標；
（2）通過上述計算，結合已學知識和經驗，猜想這些交點都在某二次函數圖象上，設交點的縱坐標為y,橫坐標為x,請求出y與x之間的函數關系式．組卷：425引用：2難度：0.5 -
23．問題情境
利用圓規旋轉探索：每位同學在紙上畫好Rt△ABC，AB=CB，∠ABC=90°，要求同學們利用圓規旋轉某一條線段，探究圖形中的結論．
問題發現
某小組將線段AB繞著點A逆時針旋轉得到線段AD，旋轉角設為α，連接CD、BD，如圖1所示．
如圖2，小李同學發現，當點D落在邊AC上時，∠BAD=2∠CBD=α．
如圖3，小王同學發現，當α每改變一個度數時，CD的長也隨之改變．
……
問題提出與解決
該小組根據小李同學和小王同學的發現，討論后提出問題1，請你解答．
問題1：如圖1，在Rt△ABC中，AB=CB，∠ABC=90°，將線段AB繞著點A逆時針旋轉得到線段AD，旋轉角設為α，連接CD、BD．
?
（1）如圖2，當點D落在邊AC上時，求證：2∠CBD=∠BAD=α；
（2）如圖3，當α=30°時，若，求CD的長．AB=6+2
拓展延伸
小張同學受到探究過程的啟發，將等腰三角形的頂角改為100°，嘗試畫圖，并提出問題2，請你解答．
問題2：如圖4，△ABC中，AB=CB，∠ABC=100°，將線段AB繞著點A逆時針旋轉得到線段AD，旋轉角α=20°，連接CD、BD，求∠ACD的度數．組卷：279引用：1難度：0.3