2023年浙江省舟山市中考數學三模試卷

一、選擇題（本題有10小題，每小題3分，共30分．請選出各題中唯一的正確選項，不選、多選、錯選，均不給分）

• 1．下列各數中，為無理數的是（　　）

  A． - 32 7

  B．1

  C． 3

  D． 3 . . 5
  組卷：15引用：1難度：0.8

  解析

• 2．下列計算中，正確的是（　　）

  A．a3÷a2=a	B．a2?a4=a8
  C．（-ab2）2=-a2b4	D．（x-y）2=x2-y2
  組卷：21引用：1難度：0.7

  解析

• 3．若a＜b,下列各式中一定成立的是（　　）

  A．am＞bm	B． a m ＜ b m
  C．（1+m2）a＜（1+m2）b	D．1-a＜1-b
  組卷：500引用：2難度：0.7

  解析

• 4．在平面直角坐標系中，已知點A（-4，2），B（-6，-4），以原點O為位似中心，相似比為

  1

  2

  ，把△ABO縮小，則點A的對應點A′的坐標是（　　）

  A．（-2，1）	B．（2，-1）
  C．（-8，4）或（8，-4）	D．（-2，1）或（2，-1）
  組卷：538引用：9難度：0.5

  解析

• 5．如圖，某天氣預報軟件顯示“舟山市定海區明天的降水概率為85%”，對這條信息的下列說法中，正確的是（　　）

  A．定海區明天下雨的可能性較大

  B．定海區明天下雨的可能性較小

  C．定海區明天將有85%的時間下雨

  D．定海區明天將有85%的地區下雨
  組卷：75引用：1難度：0.7

  解析

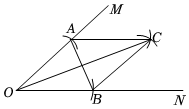• 6．如圖，在∠MON的兩邊上分別截取OA、OB，使OA=OB；分別以點A、B為圓心，OA長為半徑作弧，兩弧交于點C；連接AC、BC、AB、OC．若AB=2cm,四邊形AOBC的面積為8cm²．則OC的長為（　　）
  

  A．5cm

  B．8cm

  C．10cm

  D．4cm
  組卷：54引用：1難度：0.7

  解析

• 7．數學家吳文俊院士非常重視古代數學家賈憲提出的“從長方形對角線上任一點作兩條分別平行于兩鄰邊的直線，則所容兩長方形面積相等（如圖所示）”這一推論，他從這一推論出發，利用“出入相補”原理復原了《海島算經》九題古證，根據圖形可知他得出的這個推論指（　　）
  

  A．S矩形ABMN=S矩形MNDC	B．S矩形EBMF=S矩形AEFN
  C．S矩形AEFN=S矩形MNDC	D．S矩形EBMF=S矩形NFGD
  組卷：171引用：2難度：0.6

  解析

• 8．如圖，一次函數y₁=x-1的圖象與反比例函數

  y

  2

  =

  k

  x

  的圖象交于點A（2，m），B（n,-2），當y₁＞y₂時，x的取值范圍是（　　）
  

  A．x＜-1或x＞2	B．x＜-1或0＜x＜2
  C．-1＜x＜0或0＜x＜2	D．-1＜x＜0或x＞2
  組卷：370引用：2難度：0.5

  解析

三、解答題（本題有8小題，第17～19題每題6分，第20，21題8分，第22、23題每題10分，第24題12分，共66分）

• 23．在平面直角坐標系中，拋物線y=x²+bx+c（b,c是常數）經過點A（1，0），點B（0，3）．點P在此拋物線上，其橫坐標為m.
  （1）求此拋物線的解析式．
  （2）若-1≤x≤d時，-1≤y≤8，則d的取值范圍是

  ．
  （3）點P和點A之間（包括端點）的函數圖象稱為圖象G，當圖象G的最大值和最小值差是5時，求m的值．
  組卷：254引用：2難度：0.5

  解析

• 24．如圖1，在⊙O中，直徑AB⊥CD于點F，點E為⊙O上一點，點C為弧AE的中點，連結AE，交CD于點G．
  （1）求證：AE=CD；
  （2）如圖2，過點C作⊙O的切線交BA的延長線于點Q，若AF=2，AE=8，求OQ的長度；
  （3）在（2）的基礎上，點P為⊙O上任一點，連結PF、PQ，

  PF

  PQ

  的比值是否發生改變？若不變，求出比值；若變化，說明變化規律．
  
  組卷：154引用：1難度：0.1

  解析