當前位置：試卷中心 > 試卷詳情

2020-2021學年福建省泉州科技中學高一（下）期中數學試卷

發布：2024/10/27 9:30:2

一、單項選擇題（本大題共8小題，每小題5分，共40分.）

1．設向量
a
=（0，2），
b
=（2，2），則（　　）
A．|
a
|=|
b
| B．（
a
-
b
）∥
b
C．
a
與
b
的夾角為
π
3
D．（
a
-
b
）⊥
a
組卷：396引用：15難度：0.7
解析
2．若復數Z=（a²-1）+（a+1）i為純虛數，a為實數，則
a
+
i
2007
1
+
ai
的值為（　　）
A．1 B．-1 C．i D．-i
組卷：426引用：3難度：0.9
解析
3．正四棱臺的上、下底面邊長分別為1cm,3cm,側棱長為2cm,則棱臺的側面積為（　　）
A．4cm² B．8cm² C．
4
3
c
m
2
D．
8
3
c
m
2
組卷：555引用：5難度：0.8
解析
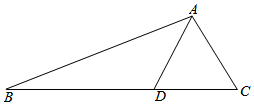4．如圖，在△ABC中，點D在BC邊上，∠ADC=60°，CD=AD=2，BD=4，則sinB的值為（　　）
A．
1
2
B．
7
6
C．
7
14
D．
21
14
組卷：292引用：6難度：0.7
解析
5．在矩形ABCD中，對角線AC分別與AB，AD所成的角為α，β，則sin²α+sin²β=1，在長方體ABCD-A₁B₁C₁D₁中，對角線AC₁與棱AB，AD，AA₁所成的角分別為α₁，α₂，α₃，與平面AC，平面AB₁，平面AD₁所成的角分別為β₁，β₂，β₃，則下列說法正確的是（　　）

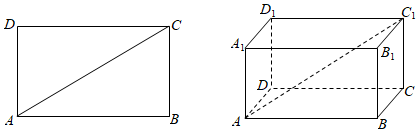
①sin²α₁+sin²α₂+sin²α₃=1
②sin²α₁+sin²α₂+sin²α₃=2
③cos²α₁+cos²α₂+cos²α₃=1
④sin²β₁+sin²β₂+sin²β₃=1
A．①③ B．②③ C．①③④ D．②③④
組卷：58引用：4難度：0.6
解析
6．我國古代人民早在幾千年以前就已經發現并應用勾股定理了，勾股定理最早的證明是東漢數學家趙爽在為《周髀算經》作注時給出的，被后人稱為“趙爽弦圖”．“趙爽弦圖”是數形結合思想的體現，是中國古代數學的圖騰，還被用作第24屆國際數學家大會的會徽．如圖，大正方形ABCD是由4個全等的直角三角形和中間的小正方形組成的，若
AB
=
a
，

AD
=
b
，E為BF的中點，則
AE
=（　　）
A．
4
5
a
+
2
5
b
B．
2
5
a
+
4
5
b
C．
4
3
a
+
2
3
b
D．
2
3
a
+
4
3
b
組卷：1095引用：21難度：0.6
解析
7．已知三棱錐P-ABC的頂點都在球O的球面上，AB=AC=2，BC=2
2
，PB⊥平面ABC，若該三棱錐的體積是
8
3
，則球O的表面積是（　　）
A．32π B．32
2
π C．24
2
π D．24π
組卷：79引用：2難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

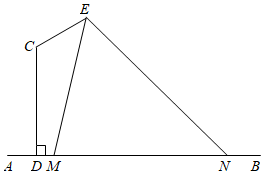21．某校要在一條水泥路邊安裝路燈，其中燈桿的設計如圖所示，AB為地面，CD，CE為路燈燈桿，CD⊥AB，∠DCE=
2
π
3
，在E處安裝路燈，且路燈的照明張角∠MEN=
π
3
．已知CD=4m,CE=2m.
（1）當M，D重合時，求路燈在路面的照明寬度MN；
（2）求此路燈在路面上的照明寬度MN的最小值．
組卷：268引用：14難度：0.7
解析
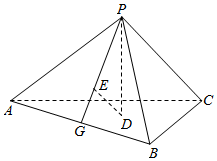22．如圖，已知正三棱錐P-ABC的側面是直角三角形，PA=6，頂點P在平面ABC內的正投影為點D，D在平面PAB內的正投影為點E，連接PE并延長交AB于點G．
（Ⅰ）證明：G是AB的中點；
（Ⅱ）在圖中作出點E在平面PAC內的正投影F（說明作法及理由），并求四面體PDEF的體積．
組卷：6870引用：14難度：0.5
解析