2010年“學而思杯”中學生理科能力大賽初一數學試卷（B卷）

一、填空題：（本題共15小題，每小題4分，共60分）

• 1．已知a、b為實數，且ab=4，設

  M

  =

  a

  2

  a

  +

  4

  +

  b

  2

  b

  +

  4

  ，

  N

  =

  1

  a

  +

  2

  +

  1

  b

  +

  2

  ，則M、N的大小關系是M

   

  N．（填“＞”、“＜”、“=”其中一個）
  組卷：198引用：1難度：0.9

  解析

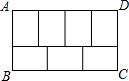• 2．如圖，長方形ABCD恰好可分成7個形狀大小相同的小長方形，如果小長方形的面積是3，則長方形ABCD的周長是

  ．
  組卷：206引用：1難度：0.9

  解析

• 3．已知a,b,c為整數，且a+b=2010，c-a=2009．若a＜b,則a+b+c的最大值為

   

  ．
  組卷：184引用：1難度：0.9

  解析

• 4．觀察下列算式：2¹=2、2²=4、2³=8、2⁴=16、2⁵=32、2⁶=64、2⁷=128、2⁸=256…．觀察后，用你所發現的規律寫出2²³的末位數字是

   

  ．
  組卷：256引用：11難度：0.5

  解析

• 5．實數a、b、c都不為0，且a+b+c=0，則

  a

  （

  1

  b

  +

  1

  c

  ）

  +

  b

  （

  1

  c

  +

  1

  a

  ）

  +

  c

  （

  1

  a

  +

  1

  b

  ）

  =

  ．
  組卷：1109引用：16難度：0.5

  解析

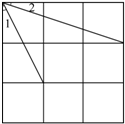• 6．如圖，正方形的網格中，∠1+∠2=

   

  ．
  組卷：96引用：1難度：0.7

  解析

二、解答題（每題10分，共40分）

• 19．已知：五位數

  abcde

  滿足下列條件：
  （1）它的各位數字均不為零；
  （2）它是一個完全平方數；
  （3）它的萬位上的數字a是一個完全平方數，千位和百位上的數字順次構成的兩位數

  bc

  以及十位和個位上的數字順次構成的兩位數

  de

  也都是完全平方數．
  試求出滿足上述條件的所有五位數．
  組卷：104引用：3難度：0.1

  解析

三、附加題（10分）

• 20．一只青蛙在平面直角坐標系上從點（1，1）開始，可以按照如下兩種方式跳躍：
  ①能從任意一點（a,b），跳到點（2a,b）或（a,2b）；
  ②對于點（a,b），如果a＞b,則能從（a,b）跳到（a-b,b）；如果a＜b,則能從（a,b）跳到（a,b-a）．
  例如，按照上述跳躍方式，這只青蛙能夠到達點（3，1），跳躍的一種路徑為：
  （1，1）→（2，1）→（4，1）→（3，1）．
  請你思考：這只青蛙按照規定的兩種方式跳躍，能到達下列各點嗎？如果能，請分別給出從點（1，1）出發到指定點的路徑；如果不能，請說明理由．
  （1）（3，5）；（2）（12，60）；（3）（200，5）；（4）（200，6）．
  組卷：137引用：3難度：0.5

  解析