當前位置：試卷中心 > 試卷詳情

2021-2022學年福建省泉州市鯉城區科技中學八年級（下）期中數學試卷

發布：2024/12/23 3:0:2

1．使分式
x
x
-
1
有意義的x必須滿足的條件是（　　）
A．x≠0 B．x≠1 C．x＞0 D．x＞1
組卷：218引用：5難度：0.9
解析
2．計算a³?（
1
a
）²的結果是（　　）
A．a B．a⁵ C．a⁶ D．a⁸
組卷：886引用：5難度：0.9
解析
3．已知在?ABCD中，∠A=∠B+40°，則∠A的度數為（　　）
A．35° B．70° C．110° D．140°
組卷：467引用：7難度：0.7
解析
4．如圖，在矩形ABCD中，E、F、G、H分別為邊AB、BC、CD、DA的中點．若AB=4，AD=6，則圖中陰影部分的面積為（　　）
A．12 B．6 C．24 D．3
組卷：99引用：2難度：0.6
解析
5．化簡
x
2
x
-
1
-
x
x
-
1
的結果是（　　）
A．x+1 B．x-1 C．x D．-x
組卷：1764引用：21難度：0.9
解析
6．分式
x
+
2
y
3
xy
中x和y同時變為原來的10倍，那么分式的值（　　）
A．不變 B．變為原來的10倍
C．變為原來的
1
10
D．變為原來的
1
100
組卷：87引用：2難度：0.9
解析
7．如圖，在?ABCD中，DE平分∠ADC，AD=6，BE=2，則?ABCD的周長是（　　）
A．16 B．14 C．20 D．24
組卷：2327引用：15難度：0.9
解析
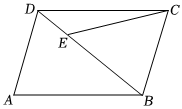8．如圖，在?ABCD中，AB=BD，點E在BD上，CE=CB．如果∠ADB=65°，那么∠DCE等于（　　）
A．20° B．15° C．30° D．35°
組卷：191引用：3難度：0.6
解析

24．如圖，在Rt△ABC中，∠ABC=90°，DH垂直平分AB交AC于點E，連接BE、CD，且CD=CE．
（1）如圖1，求證：四邊形BCDE是平行四邊形；
（2）如圖2，點F在AB上，且BF=BC，連接BD，若BD平分∠ABC，試判斷DF與AC的位置關系，并證明你的結論．
組卷：2268引用：6難度：0.1
解析
25．材料閱讀：中位線是一個數學術語，是平面幾何內的三角形任意兩邊中點的連線或梯形兩腰中點的連線．而在三角形中，它的中位線平行于第三邊，并且等于第三邊的一半．例：如圖1，在△ABC中，若D、E分別是AB、AC的中點，則DE為△ABC的中位線，并且DE∥BC，DE=
1
2
BC．請根據材料，完成以下問題：
（1）如圖2，在△ABC中，AB=AC，且D、E、F分別是邊AB、AC、BC的中點，分別連接DE、EF、FD．證明：四邊形ADFE是菱形．
（2）如圖3，已知正方形ABCD，點F是射線DC上一動點（不與C、D重合）．連接AF并延長交直線BC于點E，交BD于H，連接CH，過點C作CG⊥HC交AE于點G．
①若點F在邊CD上，如圖3，猜想△GFC的形狀并說明理由．
②取DF中點M，連接MG．若MG=2.5，正方形邊長為4，求BE的長．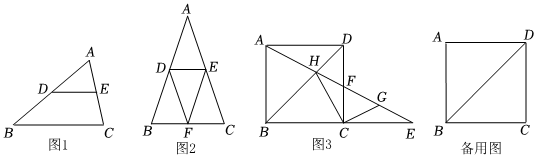
組卷：319引用：2難度：0.1
解析