2005年湖南省岳陽市巴陵石化系統九年級數學競賽試卷（華師大版）

一、填空題（共6小題，每小題5分，滿分30分）

• 1．若1000張獎券中有200張可以中獎，則從中任抽1張能中獎的概率為

  ．
  組卷：22引用：38難度：0.7

  解析

• 2．若實數m,n滿足條件m+n=3，且m-n=1，則m=

  ，n=

  ．
  組卷：95引用：17難度：0.7

  解析

• 3．在△ABC中，若D、E分別是邊AB、AC上的點，且DE∥BC，AD=1，DB=2，則△ADE與△ABC的面積比為

  ．
  組卷：97引用：16難度：0.5

  解析

• 4．函數y=

  1

  -

  2

  x

  1

  +

  x

  的自變量x的取值范圍是

   

  ．
  組卷：60引用：10難度：0.9

  解析

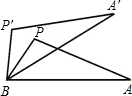• 5．如圖，如果△APB繞點B按逆時針方向旋轉30°后得到△A′P′B，且BP=2，那么PP′的長為

   

  ．（不取近似值．以下數據供解題使用：sin15°=

  6

  -

  2

  4

  ，cos15°=

  6

  +

  2

  4

  ）
  組卷：642引用：35難度：0.5

  解析

• 6．已知n（n≥2）個點P₁，P₂，P₃，…，P_n在同一平面內，且其中沒有任何三點在同一直線上．設S_n表示過這n個點中的任意2個點所作的所有直線的條數，顯然，S₂=1，S₃=3，S₄=6，S₅=10，…，由此推斷，S_n=

  ．
  組卷：1976引用：9難度：0.5

  解析

三、解答題（共4小題，滿分50分）

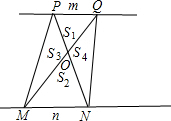• 19．如圖，若梯形PMNQ是一塊綠化地，梯形上底PQ=m,下底MN=n,現在計劃把價格不同的兩種花草種植在S₁、S₂、S₃、S₄四塊地里，使得價格相同的花草不相鄰，為了節省費用，園藝師應該把哪兩塊地種植較便宜的花草？通過計算說明你的理由．
  組卷：209引用：1難度：0.1

  解析

• 20．已知∠B為△ABC的內角，且sinB與cosB恰好為方程mx²-mx+p-4=0的兩根，以AB為直徑的⊙O交AC于D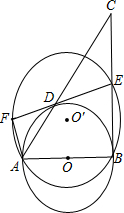，取BC的中點E，經過A、B、E的⊙O′交直線DE于F，如圖，連接AF．
  （1）求證：EF為⊙O的切線；
  （2）求證：AD²=AF?AB；
  （3）若⊙O的半徑R=p,且AD：CD=2：3，求弦EF的長及tan∠ABF．
  組卷：60引用：1難度：0.5

  解析