2020-2021學年四川省樂山市井研縣八年級（上）期末數學試卷

一、選擇題。（每小題3分，共36分）下列各題所給答案中，有且只有一個答案是正確的.

• 1．4的平方根是（　　）

  A．±16

  B．± 2

  C．±2

  D． 2
  組卷：400引用：18難度：0.9

  解析

• 2．下列運算結果正確的是（　　）

  A．a2+a2=2a4	B．a6÷a2=a3
  C．（-a2）3=-a6	D．（a-2）（a+3）=a2-6
  組卷：7引用：1難度：0.6

  解析

• 3．為了便于看出各部分在總體中所占的比例，選用以下哪種統計圖比較合適（　　）

  A．條形統計圖	B．折線統計圖
  C．扇形統計圖	D．頻數分布直方圖
  組卷：9引用：1難度：0.7

  解析

• 4．已知x-2的立方根為2，2x+y的算術平方根為5，則x+y的值為（　　）

  A．19

  B．15

  C．8

  D．5
  組卷：12引用：1難度：0.8

  解析

• 5．在下列命題中，逆命題是假命題的是（　　）

  A．相等的角是對頂角

  B．到線段兩端距離相等的點在這條線段的垂直平分線上

  C．全等三角形的對應角相等

  D．角平分線上的點到這個角兩邊的距離相等
  組卷：14引用：1難度：0.6

  解析

• 6．兩只小鼴鼠在地下打洞，一只朝正東方向挖，每分鐘挖8cm,另一只朝正南方向挖，每分鐘挖6cm,10分鐘后兩只小鼴鼠相距（　　）

  A．140cm

  B．100cm

  C．80cm

  D．50cm
  組卷：20引用：1難度：0.9

  解析

• 7．已知x^m=2，xⁿ=3，則x^2m-3n的值為（　　）

  A．-5

  B． 4 27

  C． 4 9

  D．-23
  組卷：63引用：2難度：0.9

  解析

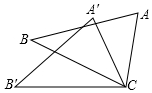• 8．如圖，△ACB≌△A′CB′，∠BCB′=25°，則∠ACA′的度數為（　　）

  A．35°

  B．30°

  C．25°

  D．20°
  組卷：148引用：2難度：0.7

  解析

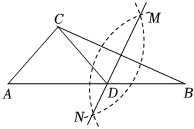• 9．如圖，在已知△ABC中，按以下步驟作圖：①分別以B，C為圓心，以大于

  1

  2

  BC的長為半徑作弧，兩弧相交于兩點M，N；②作直線MN交AB于點D，連接CD．若CD=CA，∠B=25°，則∠A的度數為（　　）

  A．50°

  B．45°

  C．25°

  D．65°
  組卷：37引用：1難度：0.5

  解析

• 10．若x²+y²=13，xy=6，則x+y與x-y的值分別是（　　）

  A．5，1

  B．-5，-1

  C．5，±1

  D．±5，±1
  組卷：19引用：1難度：0.6

  解析

六、綜合與實踐。（第29小題10分，第30小題12分，共22分）

• 29．請閱讀以下材料，并解決問題：
  配方法是一種重要的數學方法，它是指將一個式子或一個式子的某一部分通過恒等變形化為完全平方式或幾個完全平方式的和的方法．這種方法常被用到代數恒等變形中，并結合非負數的性質來解決一些問題．例如對于式子x²+2x-3可以變形如下：
  原式=x²+2x+1-1-3=（x²+2x+1）-4=（x+1）²-4，此種變形抓住了完全平方公式的特點，先加一項，使這三項成為完全平方式，再減去加的項，這種變形方法就是配方法．我們還可以進一步求x²+2x-3的最小值，∵（x+1）²≥0，∴（x+1）²-4≥4，∴x²+2x-3的最小值是-4．
  （1）若x²-4x+5可配方成（x-m）²+n（m,n為常數）的形式，求m和n的值；
  （2）求代數式x²+6x+y²-10y+40的最小值；
  （3）若實數x,y滿足x²+3x+y-5=0，那么代數式x+y是否存在最大值或最小值？如果存在，求出它的最大值或最小值；如果不存在，請說明理由．
  組卷：80引用：1難度：0.6

  解析

• 30．（1）【問題發現】如圖，△ABC為等邊三角形，點D為邊BC上一動點，（不與B、C重合），以AD為邊作等邊△ADE（頂點A、D、E按逆時針方向排列），連結CE，則：①∠ACE的度數是

  ；②線段AC、CD、CE的數量關系是

  ；
  （2）【拓展探究】如圖2，△ABC為等腰直角三角形，∠BAC=90°，點D為邊BC上一動點，（不與B、C重合），以AD為邊作等腰Rt△ADE，且∠DAE=90°，連結CE，請求出∠ACE的度數及線段BD、CD、DE的數量關系；
  （3）【解決問題】在（2）問的條件下，當AD=CE=1時，請求出AC的長度．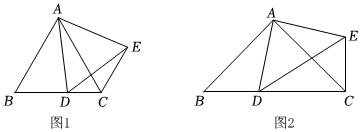
  
  組卷：56引用：1難度：0.4

  解析