2010-2011學(xué)年浙江省寧波市慈溪市部分學(xué)校八年級（下）數(shù)學(xué)競賽試卷

一、選擇題（每小題4分，共24分）

• 1．在一個不透明的口袋中放著紅色、黑色、黃色的橡皮球共有30個，它們除顏色外其它全相同．小剛通過多次摸球試驗后發(fā)現(xiàn)從中摸到紅色球或黃色球的頻率穩(wěn)定在0.15和0.45之間，則口袋中黑色球的個數(shù)可能是（　　）

  A．14

  B．20

  C．9

  D．6
  組卷：134引用：4難度：0.9

  解析

• 2．已知點A的坐標為（2，3），O為坐標原點，連接OA，將線段OA繞點O按逆時針方向旋轉(zhuǎn)90°得OA₁，再將點A₁作關(guān)于x軸對稱得到A₂，則A₂的坐標為（　　）

  A．（-2，3）

  B．（-2，-3）

  C．（-3，-2）

  D．（3，2）
  組卷：99引用：4難度：0.9

  解析

• 3．若不等式組

  x + a ≥ 0

  1 - 2 x ＞ x - 2

  有解，則a的取值范圍是（　　）

  A．a(chǎn)＞-1

  B．a(chǎn)≥-1

  C．a(chǎn)≤1

  D．a(chǎn)＜1
  組卷：5100引用：111難度：0.7

  解析

• 4．一些完全相同的小正方體搭成一個幾何體，這個幾何體從正面和左面看所得的平面圖形均如圖所示，小正方體的塊數(shù)可能有（　　）

  A．7種

  B．8種

  C．9種

  D．10種
  組卷：2506引用：6難度：0.1

  解析

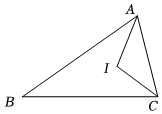• 5．如圖，在△ABC中，∠BAC、∠BCA的平分線相交于點I，若∠B=35°，BC=AI+AC，則∠BAC的度數(shù)為（　　）

  A．60°

  B．70°

  C．80°

  D．90°
  組卷：1389引用：6難度：0.3

  解析

• 6．如圖，△AP₁B中，BP₁⊥AP₁，AP₁=2，∠A=30°，P₁Q₁⊥AB，Q₁P₂⊥AP₁，P₂Q₂⊥AB，Q₂P₃⊥AP₁…，P_nQ_n⊥AB，P_n+1Q_n⊥AP₁，則S=P₁Q₁+P₂Q₂+…+P_nQ_n+…的值為（　　）

  A．2

  B．3

  C．4

  D．8
  組卷：55引用：2難度：0.9

  解析

三、解答題（共四小題，46分）

• 19．閱讀以下的材料：
  如果兩個正數(shù)a,b,即a＞0，b＞0，則有下面的不等式：

  a

  +

  b

  2

  ≥

  ab

  ，當且僅當a=b時取到等號
  我們把

  a

  +

  b

  2

  叫做正數(shù)a,b的算術(shù)平均數(shù)，把

  ab

  叫做正數(shù)a,b的幾何平均數(shù)，于是上述不等式可表述為：兩個正數(shù)的算術(shù)平均數(shù)不小于（即大于或等于）它們的幾何平均數(shù)．它在數(shù)學(xué)中有廣泛的應(yīng)用，是解決最大（小）值問題的有力工具，下面舉一例子：
  例：已知x＞0，求函數(shù)

  y

  =

  x

  +

  4

  x

  的最小值．
  解：令

  a

  =

  x

  ,

  b

  =

  4

  x

  ，則由

  a

  +

  b

  ≥

  2

  ab

  ，得

  y

  =

  x

  +

  4

  x

  ≥

  2

  x

  ?

  4

  x

  =

  4

  ，當且僅當

  x

  =

  4

  x

  時，即x=2時，函數(shù)有最小值，最小值為4．
  根據(jù)上面回答下列問題
  ①已知x＞0，則當x=

  時，函數(shù)

  y

  =

  2

  x

  +

  3

  x

  取到最小值，最小值為

  ；
  ②用籬笆圍一個面積為100m²的矩形花園，問這個矩形的長、寬各為多少時，所用的籬笆最短，最短的籬笆是多少？
  ③已知x＞0，則自變量x取何值時，函數(shù)

  y

  =

  x

  x

  2

  -

  2

  x

  +

  9

  取到最大值，最大值為多少？
  組卷：1364引用：11難度：0.1

  解析

• 20．將一副三角尺如圖拼接：含30°角的三角尺（△ABC）的長直角邊與含45°角的三角尺（△ACD）的斜邊恰好重合．已知AB=

  2

  3

  ，P是AC上的一個動點．
  （1）當點P運動到∠ABC的平分線上時，連接DP，求DP的長；
  （2）當點P在運動過程中出現(xiàn)PD=BC時，求此時∠PDA的度數(shù)；
  （3）當點P運動到什么位置時，以D，P，B，Q為頂點的平行四邊形的頂點Q恰好在邊BC上？求出此時?DPBQ的面積．
  組卷：3014引用：39難度：0.1

  解析