2022-2023學(xué)年山東省濰坊市、諸城市、安丘市、高密市高一（下）期中數(shù)學(xué)試卷

一、選擇題：本大題共8小題，每小題5分，共40分，在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

• 1．已知

  a

  =

  （

  1

  ，

  3

  ）

  ，

  b

  =

  （

  x

  ,

  6

  ）

  ，若

  a

  ∥

  b

  ，則x=（　　）

  A．2

  B．-2

  C．1

  D．-1
  組卷：89引用：1難度：0.8

  解析

• 2．若α是第四象限的角，則π-α是（　　）

  A．第一象限的角	B．第二象限的角
  C．第三象限的角	D．第四象限的角
  組卷：922引用：28難度：0.7

  解析

• 3．如圖，航海羅盤將圓周32等分，設(shè)圓盤的半徑為4，則其中每一份的扇形面積為（　　）

  A．2π

  B．π

  C． π 2

  D． π 4
  組卷：42引用：1難度：0.7

  解析

• 4．設(shè)

  e

  1

  ，

  e

  2

  是平面內(nèi)所有向量的一組基底，則下面四組向量中，不能作為基底的是（　　）

  A． e 1 + e 2 和 e 1 - e 2	B． 2 e 1 - 3 e 2 和 4 e 1 - 6 e 2
  C． e 1 + 2 e 2 和 2 e 1 + e 2	D． e 2 和 e 1 + e 2
  組卷：89引用：3難度：0.8

  解析

• 5．已知tanα=2，則sin²α+sinαcosα的值為（　　）

  A． 2 3

  B．1

  C． 4 5

  D． 6 5
  組卷：294引用：2難度：0.8

  解析

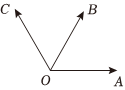• 6．如圖，已知

  OA

  ，

  OB

  ，

  OC

  的模均為4，且∠AOB=∠BOC=60°，則

  AC

  ?

  AB

  =（　　）

  A．24

  B．-24

  C．8

  D．-8
  組卷：51引用：1難度：0.8

  解析

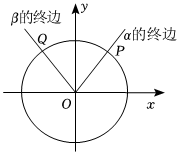• 7．如圖所示，角α的終邊與單位圓在第一象限交于點(diǎn)P，且點(diǎn)P的橫坐標(biāo)為

  3

  5

  ，OP繞O逆時(shí)針旋轉(zhuǎn)

  π

  2

  后與單位圓交于點(diǎn)Q，角β的終邊在OQ上，則（　　）

  A． sinβ = 4 5	B． cosβ = - 3 5
  C． cos （ α + β ） = 24 25	D． sin （ α + β ） = - 7 25
  組卷：61引用：1難度：0.7

  解析

四、解答題：本大題共6小題，共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟.

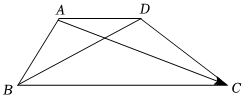• 21．如圖，在梯形ABCD中，

  AD

  =

  1

  3

  BC

  ．
  （1）令

  AB

  =

  a

  ，

  AC

  =

  b

  ，用

  a

  ，

  b

  表示

  AD

  ，

  BD

  ，

  CD

  ；
  （2）若AB=AD=2，且

  AC

  ?

  BD

  =

  12

  ，求cos∠ABC，

  |

  AC

  |

  ．
  組卷：44引用：1難度：0.5

  解析

• 22．定義函數(shù)f（x）=asinx+bcosx的“積向量”為

  m

  =

  （

  a

  ,

  b

  ）

  ，向量

  m

  =

  （

  a

  ,

  b

  ）

  的“積函數(shù)”為f（x）=asinx+bcosx.
  （1）若向量

  m

  =

  （

  a

  ,

  b

  ）

  的“積函數(shù)”f（x）滿足

  f

  （

  π

  7

  ）

  f

  （

  9

  π

  14

  ）

  =

  tan

  10

  π

  21

  ，求

  b

  a

  的值；
  （2）已知

  |

  m

  |

  =

  |

  n

  |

  =

  2

  ，設(shè)

  OP

  =

  λ

  m

  +

  μ

  n

  （

  λ

  ＞

  0

  ，

  μ

  ＞

  0

  ）

  ，且

  OP

  的“積函數(shù)”為g（x），其最大值為t,求（t-2）（λ+μ）的最小值，并判斷此時(shí)

  m

  ，

  n

  的關(guān)系．
  組卷：30引用：1難度：0.5

  解析