當前位置：試卷中心 > 試卷詳情

2020-2021學年江蘇省鹽城中學七年級（下）第二次月考數學試卷

發布：2024/4/20 14:35:0

一、選擇題。（每小題2分，共16分）

1．下列數學表達式中：①-3＜0．②2x+3y≥0，③x=1，④x²-2xy+y²，⑤x≠2，⑥x+1＞3中，不等式有（　　）
A．3個 B．4個 C．5個 D．6個
組卷：1640引用：4難度：0.7
解析
2．若x＜y,則下列式子中錯誤的是（　　）
A．x-2＜y-2 B．x+2＜y+2 C．-2x＜-2y D．
x
2
＜
y
2
組卷：42引用：1難度：0.8
解析
3．在數軸上表示不等式x+1＞0的解集，正確的是（　　）
A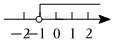． B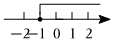． C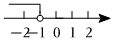． D．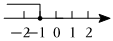
組卷：19引用：1難度：0.7
解析
4．若方程（a-5）x^|a|-4+5y=1是關于x,y的二元一次方程，則a的值為（　　）
A．±5 B．-5 C．±4 D．5
組卷：34引用：1難度：0.8
解析
5．中國古代人民在生產生活中發現了許多數學問題，在《孫子算經》中記載了這樣一個問題，大意為：有若干人乘車，若每車乘坐3人，則2輛車無人乘坐；若每車乘坐2人，則9人無車可乘，問共有多少輛車，多少人，設共有x輛車，y人，則可列方程組為（　　）
A．
3
（
x
-
2
）
=
y
2
x
+
9
=
y
B．
3
（
x
+
2
）
=
y
2
x
+
9
=
y
C．
3
x
=
y
2
x
+
9
=
y
D．
3
（
x
+
2
）
=
y
2
x
-
9
=
y
組卷：7368引用：49難度：0.5
解析
6．已知x=3-k,y=k+2，則y與x的關系是（　　）
A．y=x-1 B．x+y=1 C．x-y=2 D．x+y=5
組卷：174引用：5難度：0.7
解析
7．下列說法中，錯誤的是（　　）
A．不等式m＜2的正整數解只有一個
B．-3是不等式3m-2＜0的一個解
C．不等式-2m＞4的解集是m＞-2
D．不等式m＞2的整數解有無數個
組卷：85引用：1難度：0.5
解析
8．已知a、b為非零常數，若αx+b＞0的解集是x＜
1
3
，則bx-a＞0的解集是（　　）
A．x＜
1
3
B．x＜3 C．x＞-3 D．x＜-3
組卷：92引用：1難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題。（共68分）

25．問題1：解方程組
2
x
+
3
y
=
7
①
4
（
2
x
+
3
y
）
-
y
=
27
②
該問題，將①代入②，得4×7-y=27，解得y=1，再代入求解．易發現該方法是較為簡單的方法，我們不妨稱之為“整體代入”．
問題2：已知
3
x
-
y
=
3
①
2
x
+
5
y
=
6
②
，求x-6y的值．
本題可以通過適當變形整體求得代數式的值，由①一②便可得x-6y=-3，我們稱之為“整體加減”．“整體代入”、“整體加減”體現的數學思想，我們稱之為“整體思想”．
請解決以下問題：
（1）解方程組
x
+
y
=
2018
x
+
y
2
-
5
y
=
1094
；
（2）應用：若關于x,y的二元一次方程組
3
x
-
2
y
=
1
+
2
a
4
y
-
6
x
3
-
2
x
=
3
的解中的x是正數，求a的取值范圍；
（3）小明從家到學校上學，有一段上坡路，一段平路，一段下坡路，需用20分鐘，放學原路返回家，需用35分鐘，已知小明上坡速度3公里/小時，平路4公里/小時，下坡6公里/小時，求小明從家到學校路程幾公里？
組卷：159引用：1難度：0.5
解析
26．閱讀理解：我們知道，“作差法”是比較兩數（式）大小關系常用的方法之一，其依據是不等式（或等式）的性質：若x-y＞0，則x＞y；若x-y=0，則x=y；若x-y＜0，則x＜y.
例：已知A=m²+2mn,B=4mn-n²，其中m≠n,求證：A＞B．
證明：
A-B=（m²+2mn）-（4mn-n²）=m²+2mn-4mn+n²=m²-2mn+n²=（m-n）²．
∵m≠n,∴（m-n）²＞0．∴A＞B．
（1）比較大小：x²+4
4x；
（2）已知M=2019×2022，N=2020×2021，試運用上述方法比較M、N的大小，并說明理由；
（3）應用拓展
學科內應用：①請以“作差法”為研究不等關系的出發點，嘗試證明不等式具有如下性質：如果a＞b,c＞d,那么a+c＞b+d.
②嘗試用：①問的性質解決以下問題：
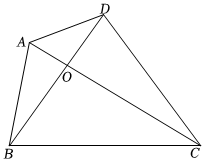
已知：四邊形ABCD是任意四邊形，AC與BD交于點O．求證：AC+BD＞
1
2
（AB+BC+CD+DA）．
生活中應用：③某游泳館在暑假期間對學生優惠開放，有A、B兩種方案可供選擇，A方案每次按原票價打八五折；B方案第一次按原票價，但從第二次起，每次打八折，請問游泳的同學選擇哪種方案更合算？
組卷：135引用：1難度：0.5
解析