2022-2023學年山西省陽泉十一中高一（上）期末數學試卷

一、單選題：本題共8小題，每小題5分，共40分．在每個小題給出的四個選項中，只有一項是符合題目要求的．

• 1．300°化為弧度制是（　　）

  A． 4 π 3

  B． 5 π 3

  C． 11 π 6

  D． 23 π 12
  組卷：489引用：4難度：0.9

  解析

• 2．設集合A={2，3，4，5，6}，B={x|-2＜x＜5}，則A∩B=（　　）

  A．{2，3}

  B．{-2＜x≤6}

  C．{2，3，4}

  D．{3，4}
  組卷：85引用：1難度：0.9

  解析

• 3．函數

  f

  （

  x

  ）

  =

  2

  +

  x

  -

  1

  x

  的定義域是（　　）

  A．[-2，0）∪（0，+∞）	B．[-2，+∞）
  C．R	D．（-∞，0）∪（0，+∞）
  組卷：331引用：1難度：0.9

  解析

• 4．“a＞2”是“

  2

  a

  ＜

  1

  ”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：226引用：1難度：0.8

  解析

• 5．已知a＞1，則

  a

  +

  9

  a

  -

  1

  的最小值為（　　）

  A．5

  B．6

  C．7

  D．10
  組卷：379引用：1難度：0.7

  解析

四、解答題：本題共3小題，每題10分，共30分．解答題應寫出文字說明、證明過程或演算步驟．

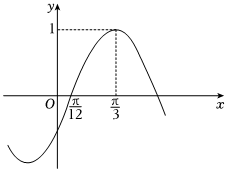• 16．已知函數

  f

  （

  x

  ）

  =

  sin

  （

  ωx

  +

  φ

  ）

  （

  ω

  ＞

  0

  ，

  |

  φ

  |

  ≤

  π

  2

  ）

  的部分圖象如圖所示．
  （1）求f（x）的解析式；
  （2）設函數

  g

  （

  x

  ）

  =

  f

  （

  x

  ）

  +

  3

  f

  （

  x

  +

  π

  4

  ）

  ，求y=g（x）的最小正周期，單調遞增區間及對稱中心．
  組卷：160引用：1難度：0.6

  解析

• 17．已知定義在R上的函數f（x）=a^x-a^-x，（a＞0且a≠1）．
  （1）若

  f

  （

  1

  ）

  =

  3

  2

  ，求f（x）的解析式，判斷其單調性并證明．
  （2）判斷f（x）奇偶性并證明．
  （3）求不等式

  f

  （

  x

  ）

  ＞

  3

  2

  的解．
  組卷：104引用：1難度：0.6

  解析