當前位置：試卷中心 > 試卷詳情

2023年江蘇省常州市經開初級中學中考數學模擬試卷（二）

發布：2024/7/15 8:0:9

一、選擇題（本題共8小題，每小題2分，共16分，在每小題所給的四個選項中，只有一個選項

1．2的倒數是（　　）
A．-
1
2
B．-2 C．
1
2
D．2
組卷：976引用：44難度：0.9
解析
2．下列計算正確的是（　　）
A．2a²-a²=1 B．（ab）²=ab² C．a²+a³=a⁵ D．（a²）³=a⁶
組卷：757引用：9難度：0.9
解析
3．下列圖形中，能通過折疊圍成一個三棱柱的是（　　）
A． B． C． D．
組卷：1808引用：77難度：0.9
解析
4．一次函數y=x+2的圖象與y軸的交點坐標為（　　）
A．（0，2） B．（0，-2） C．（2，0） D．（-2，0）
組卷：2803引用：20難度：0.9
解析
5．若a＜b,則下列結論不一定成立的是（　　）
A．a-1＜b-1 B．2a＜2b C．-
a
3
＞-
b
3
D．a²＜b²
組卷：3591引用：60難度：0.9
解析
6．估算
62
-2的值應在（　　）
A．5和6之間 B．6和7之間 C．7和8之間 D．8和9之間
組卷：994引用：9難度：0.8
解析
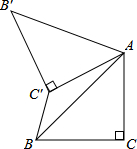7．如圖，△ABC中，∠C=90°，AC=BC=
2
，將△ABC繞點A順時針方向旋轉60°到△AB'C'的位置，連接C'B，則C'B的長為（　　）
A．
2
-
2
B．
3
2
C．
3
-
1
D．1
組卷：1716引用：12難度：0.7
解析
8．如圖，拋物線y=ax²+bx+c（a≠0）的對稱軸為直線x=-2，拋物線與x軸的一個交點在（-3，0）和（-4，0）之間，其部分圖象如圖所示．有下列結論：①4a-b=0；②c＜0；③-3a+c＞0；④4a-2b≥at²+bt（t為實數）；⑤若
（
-
9
2
，
y
1
）
，
（
-
5
2
，
y
2
）
，
（
-
1
2
，
y
3
）
是該拋物線上的三點，則y₁＜y₂＜y₃．其中，正確結論的序號有（　　）
?
A．①②③④ B．①②④⑤ C．①②③⑤ D．①②④
組卷：545引用：2難度：0.6
解析

二、填空題（本題共10小題，每小題2分，共20分）

9．計算：|-2|+2=
．
組卷：669引用：3難度：0.9
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本題共10小題，共84分）

27．在平面直角坐標系xOy中，對于任意兩點P₁（x₁，y₁）與P₂（x₂，y₂）的“非常距離”，給出如下定義：
若|x₁-x₂|≥|y₁-y₂|，則點P₁與點P₂的“非常距離”為|x₁-x₂|；
若|x₁-x₂|＜|y₁-y₂|，則點P₁與點P₂的“非常距離”為|y₁-y₂|．
例如：點P₁（1，2），點P₂（3，5），因為|1-3|＜|2-5|，所以點P₁與點P₂的“非常距離”為|2-5|=3，也就是圖1中線段P₁Q與線段P₂Q長度的較大值（點Q為垂直于y軸的直線P₁Q與垂直于x軸的直線P₂Q交點）．
（1）已知點A（-
1
2
，0），B為y軸上的一個動點，
①若點A與點B的“非常距離”為2，寫出一個滿足條件的點B的坐標；
②直接寫出點A與點B的“非常距離”的最小值；
（2）已知C是直線y=
3
4
x+3上的一個動點，
①如圖2，點D的坐標是（0，1），求點C與點D的“非常距離”的最小值及相應的點C的坐標；
②如圖3，E是以原點O為圓心，1為半徑的圓上的一個動點，求點C與點E的“非常距離”的最小值及相應的點E與點C的坐標．
組卷：867引用：26難度：0.2
解析
28．如圖①，在平面直角坐標系xOy中，A是第一象限內一點，過點A的直線分別與x軸、y軸的正半軸交于M，N兩點，且A是MN的中點，以OA為直徑的⊙T交直線MN于點B（位于點A右下方），交y軸于點C，連接BC交OA于點K．
（1）若點A的坐標為（1，2），請直接寫出M，N兩點的坐標和AB的長；
（2）若
OK
KA
=
3
，求∠AON的度數；
（3）如圖②，P是
?
BOC
上一點，在（2）的條件下，若四邊形ABPC的面積是
3
3
，記PC=m.
①用含m的代數式表示PB；
②求當
S
△
PBC
+
3
2
PC
取最大值時⊙T的半徑．
組卷：110引用：1難度：0.1
解析