2022-2023學年內蒙古阿拉善盟一中高一(下)期中數學試卷
發布:2024/6/15 8:0:9
一、單項選擇題:本題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的。
-
1.已知向量
,且a=(2,4),b=(1,x),則x=( )a∥bA.2 B.-2 C.8 D.-8 組卷:85引用:5難度:0.9 -
2.命題“?a∈[0,+∞),sina>a”的否定形式是( )
A.?a∈[0,+∞),sina≤a B.?a∈[0,+∞),sina≤a C.?a∈(-∞,0),sina≤a D.?a∈(-∞,0),sina>a 組卷:64引用:4難度:0.9 -
3.設全集U={1,2,3,4,5,6,7},集合A={1,3,5},集合B={3,5},則( )
A.U=A∪B B.U=(?UA)∪B C.U=A∪(?UB) D.U=(?UA)∪(?UB) 組卷:66引用:19難度:0.9 -
4.已知單位向量
,a滿足|b-a|=b,則cos<3,a+a>=( )bA. -12B. 12C. 32D. -32組卷:255引用:4難度:0.8 -
5.在△ABC中,a,b,c分別為內角A,B,C所對的邊長,若c2=(a-b)2+6,
,則△ABC的面積是( )C=π3A.3 B. 932C. 332D.3 3組卷:230引用:4難度:0.9 -
6.在△ABC中,D為BC的中點,E為AC邊上的點,且
,則AE=3EC=( )EDA. -12AB+14ACB. 12AB-23ACC. 12AB-14ACD. -12AB+23AC組卷:484引用:12難度:0.8 -
7.設a=
cos6°-12sin6°,b=32,c=2tan13°1+tan213°,則有( )1-cos50°2A.a>b>c B.a<b<c C.b<c<a D.a<c<b 組卷:862引用:37難度:0.9
四、解答題(本大題共有6小題,共70分.解答應寫出必要的文字說明、證明過程或演算步驟.注意:答在試卷上無效)
-
21.已知向量
,a=(2sin(ωx+π4),-3,)(ω>0),函數b=(sin(ωx+π4),cos2ωx),f(x)的最小正周期為π.f(x)=a?b-1
(1)求f(x)的解析式;
(2)方程f(x)-2n+1=0在上有且只有一個解,求實數n的取值范圍.[0,7π12]組卷:18引用:3難度:0.5 -
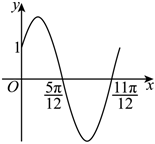 22.已知函數的部分圖象如圖所示.f(x)=Asin(ωx+φ)(ω>0,0<φ<π2)
22.已知函數的部分圖象如圖所示.f(x)=Asin(ωx+φ)(ω>0,0<φ<π2)
(1)求函數f(x)的解析式;
(2)將f(x)圖象上所有的點向左平移個單位長度,得到函數y=g(x)的圖象,若對于任意的x1,x2∈[π-m,m],當x1>x2時,f(x1)-f(x2)<g(x1)-g(x2)恒成立,求實數m的最大值.π4組卷:391引用:8難度:0.5


