2023-2024學年北京市海淀區首都師大附中七年級（上）月考數學試卷（10月份）

一、選擇題（共10小題，每小題3分，共30分）

• 1．7的相反數是（　　）

  A． 1 7

  B． - 1 7

  C．7

  D．-7
  組卷：552引用：24難度：0.8

  解析

• 2．據報道，2023年“五一”假期全國國內旅游出游合計274000000人次．數字274000000用科學記數法表示是（　　）

  A．27.4×107

  B．2.74×108

  C．0.274×109

  D．2.74×109
  組卷：1449引用：26難度：0.9

  解析

• 3．下列各式中，計算結果為1的是（　　）

  A．-（-1）

  B．-|-1|

  C．（-1）3

  D．-14
  組卷：819引用：18難度：0.8

  解析

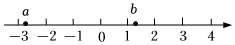• 4．有理數a,b在數軸上的對應點的位置如圖所示，下列結論中正確的是（　　）

  A．a＞-2

  B．ab＞0

  C．-a＜b

  D．|a|＞|b|
  組卷：4717引用：50難度：0.7

  解析

• 5．如圖所示的程序計算，若開始輸入的值為

  -

  1

  2

  ，則輸出的結果y是（　　）
  

  A．25

  B．30

  C．45

  D．40
  組卷：2255引用：24難度：0.6

  解析

• 6．若|m|=5，|n|=2，且m、n異號，則|m-n|的值為（　　）

  A．7

  B．3或-3

  C．3

  D．7或3
  組卷：6009引用：55難度：0.7

  解析

• 7．定義一種新運算：a*b=a²-3b,如2*1=2²-3×1=1，則（3*2）*（-1）的結果為（　　）

  A．6

  B．12

  C．-12

  D．-6
  組卷：1049引用：8難度：0.7

  解析

• 8．有理數m,n,k在數軸上的對應點的位置如圖所示，若m+n＜0，n+k＞0，則A，B，C，D四個點中可能是原點的是（　　）
  

  A．A點

  B．B點

  C．C點

  D．D點
  組卷：1161引用：30難度：0.7

  解析

三.解答題（第21題16分，第22、23題每題4分，第24題5分，第25題6分，

• 25．先閱讀下面材料，再完成任務：
  【材料】
  下列等式：4-

  3

  5

  =

  4

  ×

  3

  5

  +1，7-

  3

  4

  =

  7

  ×

  3

  4

  +1，…，具有a-b=ab+1的結構特征，我們把滿足這一特征的一對有理數稱為“共生有理數對”，記作（a,b）．例如：

  （

  4

  ，

  3

  5

  ）

  、

  （

  7

  ，

  3

  4

  ）

  都是“共生有理數對”．
  【任務】
  （1）在兩個數對（-2，1）、

  （

  2

  ，

  1

  3

  ）

  中，“共生有理數對”是

  ．
  （2）請再寫出一對“共生有理數對”

  ；（要求：不與題目中已有的“共生有理數對”重復）
  （3）若（x,-2）是“共生有理數對”，求x的值；
  （4）若（m,n）是“共生有理數對”，判斷（-n,-m）是不是“共生有理數對”，并說明理由．
  組卷：1229引用：6難度：0.5

  解析

• 26．在數軸上有A，B兩點，點B表示的數為b.對點A給出如下定義：當b≥0時，將點A向右移動2個單位長度，得到點P；當b＜0時，將點A向左移動|b|個單位長度，得到點P．稱點P為點A關于點B的“聯動點”．如圖，點A表示的數為-1．
  （1）在圖中畫出當b=4時，點A關于點B的“聯動點”P；
  （2）點A從數軸上表示-1的位置出發，以每秒1個單位的速度向右運動．點B從數軸上表示7的位置同時出發，以相同的速度向左運動，兩個點運動的時間為t秒．
  ①點B表示的數為

  （用含t的式子表示）；
  ②是否存在t,使得此時點A關于點B的“聯動點”P恰好與原點重合？若存在，請求出t的值；若不存在，請說明理由．
  組卷：767引用：4難度：0.6

  解析