2020學年人教新版九年級上學期《24.2.1 點和圓的位置關系》中考真題套卷（1）

一、選擇題（共10小題）

• 1．在△ABC中，若O為BC邊的中點，則必有：AB²+AC²=2AO²+2BO²成立．依據以上結論，解決如下問題：如圖，在矩形DEFG中，已知DE=4，EF=3，點P在以DE為直徑的半圓上運動，則PF²+PG²的最小值為（　　）

  A． 10

  B． 19 2

  C．34

  D．10
  組卷：4086引用：24難度：0.9

  解析

• 2．用反證法證明時，假設結論“點在圓外”不成立，那么點與圓的位置關系只能是（　　）

  A．點在圓內	B．點在圓上
  C．點在圓心上	D．點在圓上或圓內
  組卷：1066引用：11難度：0.9

  解析

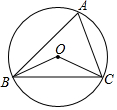• 3．有一題目：“已知：點O為△ABC的外心，∠BOC=130°，求∠A．”嘉嘉的解答為：畫△ABC以及它的外接圓O，連接OB，OC．如圖，由∠BOC=2∠A=130°，得∠A=65°．而淇淇說：“嘉嘉考慮的不周全，∠A還應有另一個不同的值．”下列判斷正確的是（　　）

  A．淇淇說得對，且∠A的另一個值是115°

  B．淇淇說的不對，∠A就得65°

  C．嘉嘉求的結果不對，∠A應得50°

  D．兩人都不對，∠A應有3個不同值
  組卷：3013引用：40難度：0.8

  解析

• 4．邊長為2的正三角形的外接圓的半徑是（　　）

  A．2 3

  B．2

  C． 2 3 3

  D． 3 2
  組卷：689引用：13難度：0.8

  解析

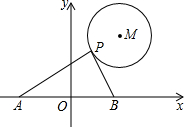• 5．如圖，⊙M的半徑為2，圓心M的坐標為（3，4），點P是⊙M上的任意一點，PA⊥PB，且PA、PB與x軸分別交于A、B兩點，若點A、點B關于原點O對稱，則AB的最小值為（　　）

  A．3

  B．4

  C．6

  D．8
  組卷：8765引用：44難度：0.7

  解析

• 6．公元前5世紀，畢達哥拉斯學派中的一名成員希伯索斯發現了無理數

  2

  ，導致了第一次數學危機，

  2

  是無理數的證明如下：
      假設

  2

  是有理數，那么它可以表示成

  q

  p

  （p與q是互質的兩個正整數）．于是（

  q

  p

  ）²=（

  2

  ）²=2，所以，q²=2p²．于是q²是偶數，進而q是偶數，從而可設q=2m,所以（2m）²=2p²，p²=2m²，于是可得p也是偶數．這與“p與q是互質的兩個正整數”矛盾．從而可知“

  2

  是有理數”的假設不成立，所以，

  2

  是無理數．
  這種證明“

  2

  是無理數”的方法是（　　）

  A．綜合法

  B．反證法

  C．舉反例法

  D．數學歸納法
  組卷：1071引用：14難度：0.7

  解析

三、解答題（共5小題）

• 19．已知：如圖，⊙O是△ABC的外接圓，

  ?

  AB

  =

  ?

  AC

  ，點D在邊BC上，AE∥BC，AE=BD．
  （1）求證：AD=CE；
  （2）如果點G在線段DC上（不與點D重合），且AG=AD，求證：四邊形AGCE是平行四邊形．
  組卷：5288引用：9難度：0.3

  解析

• 20．如圖，D是△ABC外接圓上的動點，且B，D位于AC的兩側，DE⊥AB，垂足為E，DE的延長線交此圓于點F．BG⊥AD，垂足為G，BG交DE于點H，DC，FB的延長線交于點P，且PC=PB．
  （1）求證：BG∥CD；
  （2）設△ABC外接圓的圓心為O，若AB=

  3

  DH，∠OHD=80°，求∠BDE的大小．
  
  組卷：4087引用：7難度：0.3

  解析