2023年河北省保定市部分高中高考數學三模試卷

一、單項選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知

  A

  =

  {

  x

  |

  lo

  g

  2

  1

  x

  ＜

  2

  ）

  ，B={x|x²-x-2≤0}，則（?_RA）∩B=（　　）

  A． { x | - 1 ≤ x ≤ 1 4 }

  B． | x | - 2 ≤ x ≤ 1 4 }

  C．R

  D． { x | x ≥ 1 4 }
  組卷：56引用：1難度：0.7

  解析

• 2．設z=i²⁰²³-1（i 是虛數單位），則z²-2

  z

  =（　　）

  A．-2

  B．-2+4i

  C．2

  D．4-i
  組卷：29引用：1難度：0.8

  解析

• 3．已知直線l₁：ax-5y-1=0，l₂：3x-（a+2）y+4=0，“a=3”是“l₁∥l₂”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：78引用：5難度：0.8

  解析

• 4．已知隨機變量ξ服從正態分布N（2，σ²），且P（ξ≤0）=0.2，則P（2＜ξ≤4）等于（　　）

  A．0.8

  B．0.6

  C．0.4

  D．0.3
  組卷：76引用：3難度：0.8

  解析

• 5．已知△ABC外接圓的半徑為R，且

  a

  2

  -

  c

  2

  2

  R

  =

  （

  a

  -

  b

  ）

  sin

  B，sinB=2sinA，c=2，則△ABC的面積為（　　）

  A． 4 3

  B． 2 3 3

  C． 4 3 3

  D． 2 3
  組卷：145引用：3難度：0.6

  解析

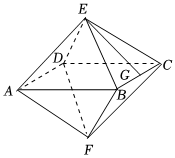• 6．正多面體被古希臘圣哲認為是構成宇宙的基本元素，加上它們的多種變體，一直是科學、藝術、哲學靈感的源泉之一．如圖，該幾何體是一個高為4的正八面體，G為BC的中點，則異面直線EG與BF所成角的正弦值為（　　）

  A． 3 6

  B． 3 2

  C． 6 3

  D． 33 6
  組卷：44引用：1難度：0.6

  解析

• 7．設O為坐標原點，點A（2，4），B在拋物線y²=2px（p＞0）上，F為焦點，M是線段BF上的點，且

  BM

  =

  2

  MF

  ，則當直線OM的斜率最大時，點F到OM的距離為（　　）

  A． 2 2

  B． 3 3

  C． 6 4

  D． 2 3 3
  組卷：125引用：1難度：0.4

  解析

四、解答題：本題共6小題，共70分.解答應寫出必要的文字說明、證明過程及演算步驟.

• 21．設橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左、右頂點分別為A，B，離心率為e,且

  |

  AB

  |

  =

  8

  3

  3

  e

  =

  4

  ．
  （1）求橢圓C的標準方程；
  （2）設點P，Q為橢圓上異于A，B的兩動點，記直線AP的斜率為k₁，直線QB的斜率為k₂，已知k₁=7k₂．直線PQ與x軸相交于點M，求△APM的面積的最大值．
  組卷：76引用：1難度：0.5

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  ax

  +

  1

  3

  x

  3

  ．
  （1）求函數f（x）的單調區間；
  （2）設g（x）=f（x）+2e^x+2cosx有兩個極值點x₁，x₂，且x₁＜x₂．
  （i）求實數a的取值范圍；
  （ii）求證：g（x₁）+g（x₂）＞8．
  組卷：94引用：3難度：0.6

  解析