2022年上海中學自主招生數學試卷

一、填空題

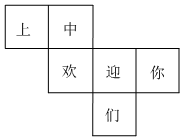• 1．如圖是正方體的一種展開圖，那么在原正方體中，與“上”字所在面相對的面上的漢字是

  ．
  組卷：170引用：2難度：0.8

  解析

• 2．下面圖1、2、3可分別用于說明

  ．
  （A、“勾股定理”；B、“平方差公式”；C、“完全平方公式”；將A、B、C按對應順序填入）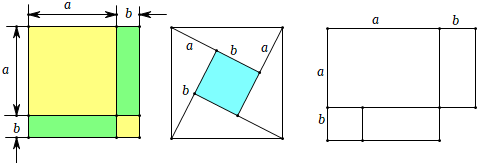
  
  組卷：142引用：1難度：0.5

  解析

• 3．使得16000?（

  2

  5

  ）ⁿ的值是一個正整數的整數n一共有

  個．
  組卷：480引用：2難度：0.4

  解析

• 4．設動直線x=t與函數y=f（x）的圖象交于點P（t,f（t）），與函數y=g（x）的圖象交于點Q（t,g（t）），當a≤t≤b時，總有PQ≤1恒成立，則稱函數f（x）與g（x）在a≤x≤b上是“逼近函數”，則下列結論：
  ①函數y=-

  x

  2

  與y=

  x

  2

  在-1≤x≤1上是“逼近函數”；
  ②函數y=5x與y=x²+5在3≤x≤4上是“逼近函數”；
  ③函數y=x²-1與y=2x²-x在0≤x≤1上是“逼近函數”，其中，正確的命題序號是

  ．
  組卷：211引用：1難度：0.7

  解析

二、解答題

• 11．有一矩形紙片ABCD，AB=a,BC=b,將矩形ABCD沿對角線AC對折后放于桌面上，探究其覆蓋桌面的面積．
  組卷：87引用：1難度：0.6

  解析

• 12．我們學習了實數與向量相乘，對于兩個非零向量

  a

  和

  b

  ，且

  a

  ∥

  b

  ，存在唯一實數λ，使得

  a

  =λ

  b

  ，記作f（

  a

  ，

  b

  ）=λ，如圖，已知A、B、C、D為同一直線上順次四點．
  （1）若f（

  AD

  ，

  DB

  ）=-2，則f（

  DB

  ，

  AD

  ）=

  ；
  （2）若

  f

  （

  AC

  ，

  CB

  ）

  f

  （

  AD

  ，

  DB

  ）

  =-1，則稱A、B、C、D為調和點列，請探究此時AB、AC、AD這三條線段的長度滿足的關系，并證明．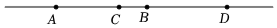
  
  組卷：137引用：1難度：0.5

  解析