2022-2023學(xué)年福建省福州八中、金山中學(xué)等九校聯(lián)考八年級（下）期中數(shù)學(xué)試卷

一、選擇題（本題共10小題，每小題4分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．下列二次根式中屬于最簡二次根式的是（　　）

  A． 2 3

  B． 3

  C． 0 . 3

  D． 12
  組卷：203引用：4難度：0.9

  解析

• 2．下列四組數(shù)據(jù)分別為四個三角形的邊長，其中是直角三角形的是（　　）

  A．2，3，4

  B．3，4，5

  C．3，5，7

  D．4，6，8
  組卷：70引用：3難度：0.8

  解析

• 3．平行四邊形ABCD中，若∠A=120°，則∠C的度數(shù)為（　　）

  A．30°

  B．60

  C．120°

  D．150°
  組卷：296引用：7難度：0.7

  解析

• 4．下列二次根式的運算正確的是（　　）

  A． 3 - 2 = 1

  B． 3 + 3 = 2 6

  C． 5 3 × 2 3 = 10 3

  D． 6 ÷ 3 = 2
  組卷：393引用：10難度：0.5

  解析

• 5．如圖，用一根繩子檢查一平行四邊形書架的側(cè)邊是否和上、下底都垂直，只需要用繩子分別測量比較書架的兩條對角線AC，BD就可以判斷，其推理依據(jù)是（　　）

  A．矩形的對角線相等

  B．矩形的四個角是直角

  C．對角線相等的四邊形是矩形

  D．對角線相等的平行四邊形是矩形
  組卷：1210引用：16難度：0.5

  解析

• 6．若菱形的兩條對角線的長分別為6和10，則菱形的面積為（　　）

  A．15

  B．24

  C．30

  D．60
  組卷：197引用：2難度：0.7

  解析

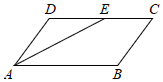• 7．如圖，在平行四邊形ABCD中，AE平分∠BAD，交CD邊于E，AD=3，AB=5，則EC的長為（　　）

  A．1

  B．2

  C．3

  D．5
  組卷：696引用：7難度：0.5

  解析

• 8．如圖，Rt△ABC中，∠B=90°，AB=4，BC=6，將△ABC折疊，使點C與AB的中點D重合，折痕交AC于點M，交BC于點N，則線段CN的長為（　　）

  A． 7 3

  B． 8 3

  C．3

  D． 10 3
  組卷：445引用：10難度：0.6

  解析

三、解答題（本題共9小題，共86分．解答應(yīng)寫出文字說明、證明過程或演算步驟）

• 24．定義：若某三角形的三邊長a,b,c滿足ab+a²=c²，則稱該三角形為“類勾股三角形”．請根據(jù)以上定義解決下列問題：
  （1）判斷等邊三角形是否為“類勾股三角形”，并說明理由；
  （2）若等腰三角形ABC是“類勾股三角形”，其中AC=BC，AB＞AC，求∠A的度數(shù)；
  （2）如圖，在△ABC中，∠C=2∠A，且∠B＞∠A．證明：△ABC為“類勾股三角形”．
  組卷：956引用：8難度：0.4

  解析

• 25．在正方形ABCD中，E是AB邊上一點（不與點A，B重合），作點D關(guān)于CE的對稱點F，連接CF．
  （1）如圖1，連接EF，若EC=EF，求證：E是AB的中點；
  （2）如圖2，連接BF，DF，作BG⊥DF于點G，M，N分別為BF，DG的中點，連接AN，MN．
  ①求∠GFB的大小；
  ②猜想線段AN與MN的關(guān)系，并證明．
  
  組卷：213引用：3難度：0.1

  解析