2023-2024學年廣東省深圳市四校聯考九年級（上）期中數學試卷
發布：2024/10/6 20:0:1
一、單選題
-
1．下列方程是一元二次方程的是（ ）
組卷：112引用：3難度：0.9 -
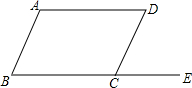2．如圖，將平行四邊形ABCD的一邊BC延長至點E．若∠A=105°，則∠BCD=（ ）組卷：97引用：2難度：0.5 -
3．給出下列判斷：
①一組對邊平行，另一組對邊相等的四邊形是平行四邊形；
②對角線相等的四邊形是矩形；
③對角線互相垂直且相等的四邊形是正方形；
④有一條對角線平分一個內角的平行四邊形為菱形．
其中，不正確的有（ ）組卷：819引用：22難度：0.9 -
4．2021年3月25日，國家衛健委新聞發言人米鋒在發布會上表示，疫情仍在全球擴散蔓延，但我國疫情已得到有效控制．新冠肺炎具有人傳人的特性，若一人攜帶病毒，未進行有效隔離，經過兩輪傳染后共有169人患新冠肺炎（假設每輪傳染的人數相同），則每輪傳染中平均每個人傳染了幾個人（ ）
組卷：647引用：3難度：0.8 -
5．某農科所在相同條件下做某作物種子發芽率的實驗，結果如表所示：
下面有四個推斷：種子個數 200 300 500 700 800 900 1000 發芽種子個數 187 282 435 624 718 814 901 發芽種子頻率 0.935 0.940 0.870 0.891 0.898 0.904 0.901
①種子個數是700時，發芽種子的個數是624．所以種子發芽的概率是0.891；
②隨著參加實驗的種子數量的增加，發芽種子的頻率在0.9附近擺動，顯示出一定的穩定性．可以估計種子發芽的概率約為0.9（精確到0.1）；
③實驗的種子個數最多的那次實驗得到的發芽種子的頻率一定是種子發芽的概率；
④若用頻率估計種子發芽的概率約為0.9，則可以估計1000kg種子大約有100kg的種子不能發芽．
其中合理的是（ ）組卷：500引用：5難度：0.7 -
6．若等腰三角形的一邊長為6，另兩邊長分別是關于x的方程x2-（k+5）x+3k+6=0的兩個根，則k的值是（ ）
組卷：760引用：4難度：0.7 -
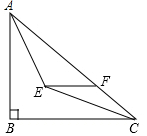7．如圖，在Rt△ABC中，∠ABC=90°，AB=6，BC=8，∠BAC，∠ACB的平分線相交于點E，過點E作EF∥BC交AC于點F，則EF的長為（ ）組卷：6932引用：20難度：0.7
三、解答題
-
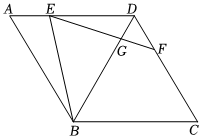21．如圖，在菱形ABCD中，∠ABC=120°，點E是AD邊上一動點，連接BE，將射線EB繞點E逆時針旋轉60°，分別交邊CD于點F，交對角線BD于點G．
（1）試判斷△ABD的形狀，并說明理由；
（2）若AB=3，AE=1，求DG及EG的長；
（3）若，求DGBG=421的值．EGGF組卷：1377引用：2難度：0.1 -
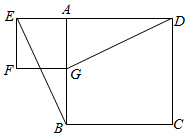22．背景：一次小組合作探究課上，小明將兩個正方形按如圖所示的位置擺放（點E、A、D在同一條直線上），發現BE=DG且BE⊥DG．
小組討論后，提出了下列三個問題，請你幫助解答：
（1）將正方形AEFG繞點A按逆時針方向旋轉（如圖1），還能得到BE=DG嗎？若能，請給出證明；若不能，請說明理由；
（2）把背景中的正方形分別改成菱形AEFG和菱形ABCD，將菱形AEFG繞點A按順時針方向旋轉（如圖2），試問當∠EAG與∠BAD的大小滿足怎樣的關系時，背景中的結論BE=DG仍成立？請說明理由；
（3）把背景中的正方形分別改寫成矩形AEFG和矩形ABCD，且，AE=4，AB=8，將矩形AEFG繞點A按順時針方向旋轉（如圖3），連接DE，BG．小組發現：在旋轉過程中，DE2+BG2的值是定值，請求出這個定值．AEAG=ABAD=23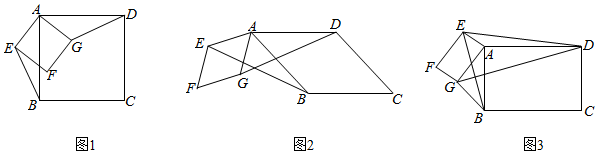
組卷：8162引用：16難度：0.3