2021-2022學年山西省太原五中九年級(上)月考數學試卷(12月份)
發布:2024/7/27 8:0:9
一、選擇題(本大題共10小題,共30分鐘)
-
1.若
=x3=y4,x=3k,y=4k,z=6k,則z6的值為( )x+zyA. 94B. 67C. 34D. 103組卷:21引用:1難度:0.7 -
2.方程x(x-1)+x-1=0的解是( )
A.x1=2,x2=1 B.x1=0,x2=-1 C.x1=0,x2=1 D.x1=-1,x2=1 組卷:378引用:4難度:0.6 -
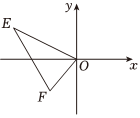 3.如圖,已知點E(-4,2),F(-2,-2),以O為位似中心,按比例尺1:2,把△EFO縮小,則點E的對應點E′的坐標為( )
3.如圖,已知點E(-4,2),F(-2,-2),以O為位似中心,按比例尺1:2,把△EFO縮小,則點E的對應點E′的坐標為( )A.(2,-1) B.(8,-4) C.(2,-1)或(-2,1) D.(8,-4)或(-8,-4) 組卷:1341引用:5難度:0.5 -
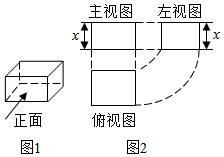 4.圖2是圖1中長方體的三視圖,用S表示面積,S主=x2+3x,S左=x2+x,則S俯=( )
4.圖2是圖1中長方體的三視圖,用S表示面積,S主=x2+3x,S左=x2+x,則S俯=( )A.x2+3x+2 B.x2+2x+1 C.x2+4x+3 D.2x2+4x 組卷:530引用:9難度:0.7 -
5.在一個不透明的袋子里裝有5個紅球和若干個白球,它們除顏色外其余完全相同,通過多次摸球試驗后發現,摸到紅球的頻率穩定在0.2附近,則估計袋中的白球大約有( )個
A.25 B.20 C.15 D.10 組卷:856引用:23難度:0.6 -
6.已知m<0,則函數y=
的圖象大致是( )m|x|A. 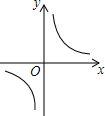
B. 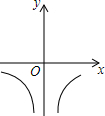
C. 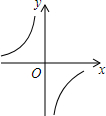
D. 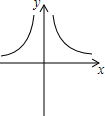 組卷:847引用:7難度:0.7
組卷:847引用:7難度:0.7 -
7.對于反比例函數y=-
,①這個函數圖象的兩個分支分別位于第二、四象限,②這個函數的圖象既是軸對稱圖形又是中心對稱圖形,③點(-2,-2)不在這個函數圖象上,④若點A(a,b)和點B(a+2,c)在該函數圖象上,則c>b.上述四個判斷中,不正確的個數是( )4xA.3 B.2 C.1 D.0 組卷:160引用:4難度:0.7
四、解答題(本大題共7小題,共65分)
-
22.閱讀與思考
下面是小明同學記錄的一節數學活動課的部分內容,請仔細閱讀,并完成相應的任務.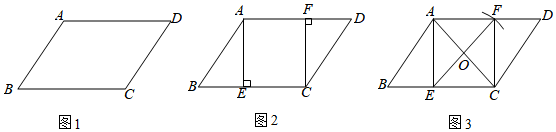
【課堂實錄】
提出問題:如圖1,請在?ABCD中畫出一個矩形并證明.
下面是小明、小亮的作法.
小明的作法如圖2,分別作AE⊥BC于點E,CF⊥AD于點F,則四邊形AECF是矩形;
證明:∵AE⊥BC、CF⊥AD,
∴∠AEC=∠AFC=90°.
∵四邊形ABCD是平行四邊形,
∴AD∥CB,
∴∠AEC+∠EAF=180°,
∴∠EAF=90°.
∴∠AEC=∠AFC=∠EAF=90°.
∴四邊形AECF是矩形.
小亮的作法如圖3,連接對角線AC,取AC的中點O,以點O為圓心,OA的長為半徑畫弧交AD于F,連接FO并延長FO交BC于點E,連接CF、AE,則四邊形AECF是矩形.
證明:∵四邊形ABCD是平行四邊形,
∴AD∥BC.
∴∠AFO=∠CEO,∠FAO=∠ECA,
…
(1)小明作法的證明依據是 是矩形.
(2)請按照上面小亮的證明思路,寫出該證明的剩余部分;
(3)如圖3,若小亮作出的矩形AECF恰好是正方形,已知AB=5,BC=7,且BE<CF,請直接寫出?ABCD的面積為 .組卷:51引用:3難度:0.4 -
23.數學活動---求重疊部分的面積.
問題情境:數學活動課上,老師出示了一個問題:
如圖1,將兩塊全等的直角三角形紙片△ABC和△DEF疊放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,頂點D與邊AB的中點重合,DE經過點C,DF交AC于點G.求重疊部分(△DCG)的面積.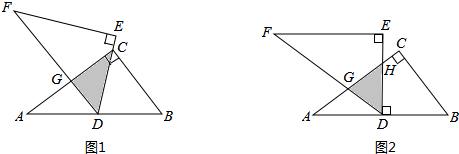
(1)獨立思考:請回答老師提出的問題.
(2)合作交流:“希望”小組受此問題的啟發,將△DEF繞點D旋轉,使DE⊥AB交AC于點H,DF交AC于點G,如圖2,你能求出重疊部分(△DGH)的面積嗎?請寫出解答過程.
(3)提出問題:老師要求各小組向“希望”小組學習,將△DEF繞點D旋轉,再提出一個求重疊部分面積的問題.
“愛心”小組提出的問題是:如圖3,將△DEF繞點D旋轉,DE,DF分別交AC于點M,N,使DM=MN,求重疊部分(△DMN)的面積.
任務:①請解決“愛心”小組提出的問題,直接寫出△DMN的面積是.
②請你仿照以上兩個小組,大膽提出一個符合老師要求的問題,并在圖4中畫出圖形,標明字母,不必解答(注:也可在圖1的基礎上按順時針旋轉).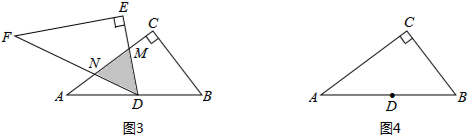 組卷:1510引用:9難度:0.1
組卷:1510引用:9難度:0.1


