2023-2024學年江西師大附中高一（上）期中數學試卷
發布：2024/10/16 5:0:1
一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．
-
1．已知集合A={y|y=2x，x≥0}，B={x∈N||2x-3|≤1}，則A∩B=（ ）
組卷：23引用：4難度：0.9 -
2．已知p：指數函數f（x）=（3a-2）x是增函數，q：
，則p是q的（ ）a＞12組卷：94引用：5難度：0.8 -
3．已知函數y=f（x）是奇函數，當x＞0時，f（x）=lnx,則
的值為（ ）f（f（1e2023））組卷：25引用：2難度：0.8 -
4．已知函數f（x）=ax-1-2（a＞0，a≠1）恒過定點M（m,n），則函數g（x）=m+xn的圖象不經過（ ）
組卷：674引用：9難度：0.8 -
5．若xlog23=1，則3x+3-x的值為（ ）
組卷：1046引用：5難度：0.8 -
6．中國與卡塔爾合建的盧塞爾體育場是世界上最大跨度的雙層索網屋面單體建筑．該體育場配備了先進的紫外線消殺污水過濾系統，已知過濾過程中污水的污染物濃度M（單位：mg/L）與時間t的關系為
（M0為最初污染物濃度）．已知前2個小時可消除30%的污染物，那么污染物消除至最初的49%共需（ ）M=M0ekt組卷：132引用：3難度：0.5 -
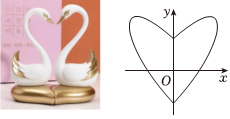7．鵝被人類稱為美善天使，它不僅象征著忠誠、長久的愛情，同時它的生命力很頑強，因此也是堅強的代表．除此之外，天鵝還是高空飛翔冠軍，飛行高度可達9千米，能飛越世界最高山峰“珠穆朗瑪峰”．如圖是兩只天鵝面對面比心的圖片，其中間部分可抽象為如圖所示的軸對稱的心型曲線．下列選項中，兩個函數的圖象拼接在一起后可大致表達出這條曲線的是（ ）組卷：98引用：5難度：0.7
四、解答題：本題共6小題，共70分．解答應寫出文字說明過程或演算步驟．
-
21．我們知道，函數y=f（x）圖像關于坐標原點成中心對稱圖形的充要條件是函數y=f（x）為奇函數，有同學發現可以將其推廣為：函數y=f（x）的圖像關于點P（m,n）成中心對稱圖形的充要條件是函數y=f（x+m）-n為奇函數．已知函數
．f（x）=44x+2
（1）利用上述結論，證明：函數f（x）的圖像關于成中心對稱圖形；（12，1）
（2）證明函數f（x）的單調性，解關于x的不等式f（ax-ax2）+f（x）＞2（a為常數且a∈R）．組卷：26引用：2難度：0.5 -
22．若函數f（x）與區間D同時滿足：①區間D為f（x）的定義域的子集；②對任意x∈D，存在常數M≥0，使得|f（x）|≤M成立；則稱f（x）是區間D上的有界函數，其中M稱為函數f（x）的一個上界．
（1）判斷函數是否是R上的有界函數；g（x）=2xx2-2x+3
（2）試探究函數在區間[0，1]上是否存在上界M，若存在，求出M的取值范圍；若不存在，請說明理由．h（x）=2+m?3x1+m?3x（m∈R）組卷：24引用：2難度：0.4