2022-2023學年廣東省深圳市寶安區松崗中學八年級（下）期中數學試卷

一、選擇題（本題共有10小題，每小題3分，共30分，每小題有四個選項，其中只有一個正確的）

• 1．三角形的三邊長分別為a、b、c,則下面四種情況中，不能判斷此三角形為直角三角形的是（　　）

  A．a=3，b=4，c=5	B．a=8，b=15，c=17
  C．a=5，b=12，c=13	D．a=12，b=15，c=18
  組卷：330引用：6難度：0.7

  解析

• 2．不等式3+2x＜1的解集在數軸上表示正確的是 （　　）

  A．

  B．

  C．

  D．
  組卷：509引用：10難度：0.8

  解析

• 3．下列各式中，從左到右的變形是因式分解的是（　　）

  A．15xy=3x?5y	B．2x2+2xy=2x（x+y）
  C．x2+x+5=x（x+1）+5	D．x2+2x+3=（x+1）2+2
  組卷：377引用：5難度：0.7

  解析

• 4．在下列不等式組中，無解的是（　　）

  A． x ＞ 1 x ＞ 2

  B． x ＞ 1 x ＜ 2

  C． x ＜ 1 x ＜ 2

  D． x ＜ 1 x ＞ 2
  組卷：1077引用：9難度：0.8

  解析

• 5．在下列正多邊形中，既是軸對稱圖形，又是中心對稱圖形的是（　　）

  A．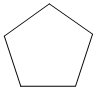

  B．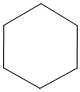

  C．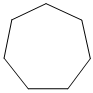

  D．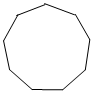
  組卷：145引用：6難度：0.8

  解析

• 6．下面是小明解不等式

  x

  +

  5

  2

  -

  1

  ＜

  3

  x

  +

  2

  2

  的過程：
  解：去分母，得x+5-1＜3x+2…①
  移項，得x-3x＜2-5+1…②
  合并同類項，得-2x＜-2…③
  兩邊同時除以-2，得x＜1…④
  小明的計算過程中，沒掌握好基本知識或粗心出錯的步驟是（　　）

  A．①②

  B．①③

  C．①④

  D．②④
  組卷：1053引用：11難度：0.7

  解析

• 7．如圖，在△ABC和△BAD中，∠C=∠D=90°．在以下條件：①AC=BD；②AD=BC；③∠BAC=∠ABD；④∠ABC=∠BAD；⑤∠CAD=∠DBC中，再選一個條件，就能使△ABC≌△BAD，共有（　　）選擇．

  A．2種

  B．3種

  C．4種

  D．5種
  組卷：1363引用：7難度：0.4

  解析

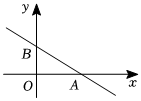• 8．如圖，一次函數y=kx+b（k≠0）的圖象分別與x軸、y軸相交A（3，0）、點B（0，2），則下列說法不正確的是（　　）

  A．當x＞3時，y＜0	B．當x＞0時，y＜2
  C．當x＜0時，y＞2	D．當x=4時，y＞0
  組卷：796引用：7難度：0.6

  解析

五、解答題三（本題共2小題，共19分）

• 24．如圖（1），已知CA=CB，CD=CE，且∠ACB=∠DCE，將△DCE繞C點旋轉（A、C、D三點在同一直線上除外）．
  （1）求證：△ACD≌△BCE；
  （2）在△DCE繞C點旋轉的過程中，若ED、AB所在的直線交于點F，當點F為邊AB的中點時，如圖2所示．求證：∠ADF=∠BEF（提示：利用類倍長中線方法添加輔助線）；
  （3）在（2）的條件下，求證：AD⊥CD．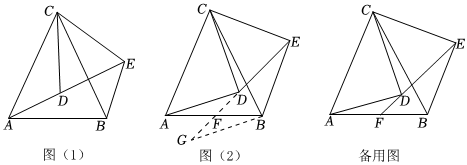
  
  組卷：1141引用：12難度：0.3

  解析

• 25．【問題背景】
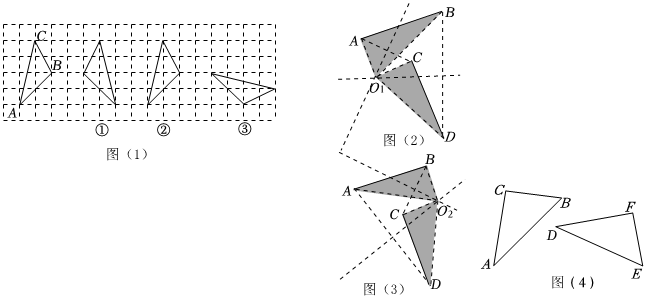
  在圖（1）中，①～③的三個三角形，各自是由△ABC通過怎樣的全等變換得到的？
  ????【問題探究】
  （1）我們發現：
  Ⅰ：圖（1）中，①號三角形能由△ABC通過一次軸對稱得到，請在圖（1）中畫出對稱軸．
  Ⅱ：圖（1）中，②號三角形能由△ABC通過一次平移得到，則平移的距離為

  單位．
  Ⅲ：圖（1）中，③號三角形能由△ABC通過先平移再旋轉或先旋轉再平移得到，請問：③號三角形能否由△ABC繞某個點，旋轉一次得到？為解決這個問題，我們可以先解決兩條相等的線段能否看成：一條線段是另一條線段繞某個點旋轉一次得到．分析過程如下：
  已知線段AB與線段CD相等，分兩種情況討論：
  

  當AB與CD對應時，如圖（2），分別作AC與BD的中垂線交于點O1，連接O1A、O1C、O1B、O1D． ∵O1在AC的中垂線上 ∴O1A=O1C 同理，O1B=O1D 又∵AB=CD ∴△ABO1≌△CDO1（SSS） ∴∠AO1B=∠CO1D ∴∠AO1C=∠BO1D，即對應點與點O1形成的夾角相等 ∴線段CD可以看成由線段AB繞點O1旋轉一次得到.

  第一種情況：
  第二種情況：當AB與DC對應時，如圖（3），同理可證．
  綜上所述：兩條相等的線段可以看成：一條線段是另一條線段繞某個點旋轉一次得到．
  【問題解決】
  （2）如圖（4），已知△ABC≌△DEF（且滿足△DEF不能由△ABC通過平移得到）．現在來解決△DEF能由△ABC繞某個點通過一次旋轉得到的問題：
  ①通過尺規作圖找到旋轉中心O；
  ②證明：△DEF能由△ABC繞點O通過一次旋轉得到．（提示：只要證明關鍵的對應點到點O的距離相等和關鍵的對應點與點O形成的夾角相等）
  組卷：367引用：5難度：0.2

  解析