2023-2024學年浙江省金衢山五校聯盟九年級（上）月考數學試卷（9月份）
發布：2024/8/20 12:0:1
一、選擇題（本題有10小題，每小題3分，共30分.請選出各題中唯一的正確選項，不選、多選、錯選，均不給分）
-
1．下列函數中，是二次函數的有（ ）
①y=3（x-1）2+1；②y=x+；③y=8x2+1；④y=3x3+2x2．1x組卷：298引用：4難度：0.7 -
2．對于二次函數y=3（x+4）2，其圖象的頂點坐標為（ ）
組卷：86引用：10難度：0.6 -
3．將拋物線y=-
（x-2）2向右平移1個單位，再向下平移2個單位后，得到的拋物線解析式為（ ）13組卷：237引用：10難度：0.7 -
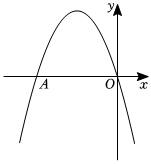4．如圖，二次函數y=ax2+bx+c的圖象與x軸交于A（-4，0）和原點，且頂點在第二象限．下列說法正確的是（ ）組卷：556引用：8難度：0.5 -
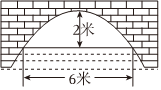5．如圖是拋物線形拱橋，當拱頂離水面2米時，水面寬6米，則當水面寬8米時，水面下降了（ ）組卷：791引用：6難度：0.5 -
6．某種品牌的服裝進價為每件150元，當售價為每件210元時，每天可賣出20件，現需降價處理，且經市場調查：每件服裝每降價2元，每天可多賣出1件．在確保盈利的前提下，若設每件服裝降價x元，每天售出服裝的利潤為y元，則y與x的函數關系式為（ ）
組卷：1988引用：9難度：0.9 -
7．已知拋物線y=-x2+2x+c,若點（0，y1）（1，y2）（3，y3）都在該拋物線上，則y1、y2、y3的大小關系是（ ）
組卷：1616引用：15難度：0.5 -
8．二次函數y=-x2+bx+c的圖象的最高點是（-1，-3），則b,c的值分別是（ ）
組卷：1491引用：6難度：0.9
三、解答題（本題有8小題，第17～19題每題6分，第20、21題每題8分，第22、23題每題10分，第24題12分，共66分）
-
23．【閱讀理解】：
關于x的函數y=mx-2m-3（m為常數，且m≠0），經過某個定點，請求出定點的坐標．
方法一：先將等式化為（x-2）m=y+3的形式，再根據0m=0時有m無數多個解，求得定點的坐標為（2，-3）；
方法二：當m=1時，y=x-5；當m=2時，y=2x-7；
解方程組解得y=x-5y=2x-7，x=2y=-3
∴求得定點的坐標為（2，-3）
【模仿練習】
關于x的二次函數 y=mx2+（2m+1）x+1（ 為常數，且m≠0），是否經過定點，如果是，請選擇一種方法求出定點的坐標；如果不是，請說明理由．
【嘗試應用】某“數學興趣小組”根據學習函數的經驗，對函數y=-（x-1）（|x|-3）的圖象和性質進行了探究，探究過程如下，請補充完整：
（1）計算x與y的幾組對應值，其中m=；
列表如下：x … -4 -3 -2 -1 0 1 2 3 4 … y … 5 0 -3 m -3 0 1 0 -3 …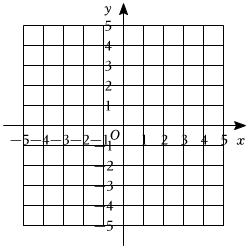 
（2）如圖，在直角坐標系中用描點法畫出了函數y=-（x-1）（|x|-3）這個圖象；
（3）若直線y=tx-2t+2與函數y=-（x-1）（|x|-3）（2＜x≤4）的圖象只有一個交點，請結合函數圖象，求出t的取值范圍．組卷：253引用：3難度：0.3 -
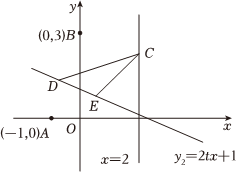24．“距離”是數學研究的重要對象，如我們所熟悉的兩點間的距離．現在我們定義一種新的距離：已知P（a,b），Q（c,d）是平面直角坐標系內的兩點，我們將|a-c|+|b-d|稱作P，Q間的“L型距離”，記作L（P，Q），即L（P，Q）=|a-c|+|b-d|．
已知二次函數y1的圖象經過平面直角坐標系內的A，B，C三點，其中A，B兩點的坐標為A（-1，0），B（0，3），點C在直線x=2上運動，且滿足L（B，C）≤BC．
（1）求L（A，B）；
（2）求拋物線y1的表達式；
（3）已知y2=2tx+1是該坐標系內的一個一次函數．
①若D，E是y2=2tx+1圖象上的兩個動點，且DE=5，求△CDE面積的最大值；
②當t≤x≤t+3時，若函數y=y1+y2的最大值與最小值之和為8，求實數t的值．組卷：533引用：4難度：0.1