2023年寧夏銀川二中北塔分校中考數學一模試卷

一、單選題（本題共8小題，每題3分，共24分）

• 1．下面的圖形是用數學家名字命名的，其中既是軸對稱圖形又是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：79引用：8難度：0.6

  解析

• 2．下列計算正確的是（　　）

  A．2x2+3x3=5x5	B．x2?x3=x6
  C．（2x2）3=6x6	D．x3÷x2=x
  組卷：245引用：4難度：0.8

  解析

• 3．2019年12月，新型冠狀病毒肺炎爆發，目前檢測出的新型冠狀病毒的半徑平均在50納米左右，即0.00000005米，用科學記數法表示0.00000005正確的是（　　）

  A．5×107

  B．5×108

  C．5×10-7

  D．5×10-8
  組卷：182引用：10難度：0.7

  解析

• 4．某市舉行“學雷鋒見行動”青少年演講比賽，時代中學要從甲、乙、丙、丁四位同學中選一名同學參加，下表是這四名同學五次校演講比賽成績統計表，如果從這四位同學中，選出一位同學參賽，那么應選的同學是（　　）
  

  	甲	乙	丙	丁
  平均分	85	90	90	85
  方差	50	42	50	42

  A．甲

  B．乙

  C．丙

  D．丁
  組卷：59引用：3難度：0.7

  解析

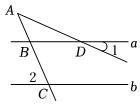• 5．如圖，直線a∥b,若∠1=24°，∠A=42°，則∠2等于（　　）

  A．66°

  B．70°

  C．42°

  D．30°
  組卷：235引用：6難度：0.7

  解析

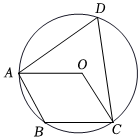• 6．如圖，點A，B，C，D在⊙O上，四邊形OABC是平行四邊形，則∠D的度數是（　　）

  A．45°

  B．50°

  C．60°

  D．65°
  組卷：192引用：7難度：0.7

  解析

• 7．在同一平面直角坐標系中，函數y=mx+m和函數y=mx²+2x+2（m是常數，且m≠0）的圖象可能是（　　）

  A．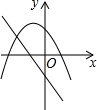

  B．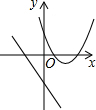

  C．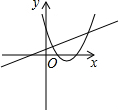

  D．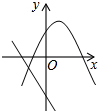
  組卷：2399引用：47難度：0.7

  解析

• 8．如圖，在矩形ABCD中，E為AB中點，以BE為邊作正方形BEFG，邊EF交CD于點H，在邊BE上取點M使BM=BC，作MN∥BG交CD于點L，交FG于點N，歐幾里得在《幾何原本》中利用該圖解釋了（a+b）（a-b）=a²-b²，現以點F為圓心，FE為半徑作圓弧交線段DH于點P，連接EP，記△EPH的面積為S₁，圖中陰影部分的面積為S₂．若點A，L，G在同一直線上，則

  S

  1

  S

  2

  的值為（　　）

  A． 2 2

  B． 2 3

  C． 2 4

  D． 2 6
  組卷：2945引用：10難度：0.5

  解析

四、解答題（本題共4小題，其中23、24每小題8分，25、26每小題8分，共36分）

• 25．在平面直角坐標系中，∠ACB=90°，AB∥x軸，如圖1，C（1，0），且OC：OA=AC：BC=1：2．
  （1）求點A、點B的坐標；
  （2）已知拋物線y=ax²+bx+c（a≠0）過A、B、C三點，求該拋物線的表達式；
  （3）如圖2，拋物線對稱軸與AB交于點D，現有一點P從點A出發，以每秒1個單位的速度在AB上向點B運動，另一點Q從點D與點P同時出發，以每秒5個單位在拋物線對稱軸上運動．當點P到達B點時，點P、Q同時停止運動，問點P、Q運動到何處時，△PQB面積最大，并求出最大面積．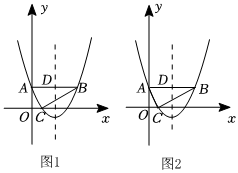
  
  組卷：276引用：2難度：0.1

  解析

• 26．我們可以通過面積運算的方法，得到等腰三角形底邊上的任意一點到兩腰的距離之和與一腰上的高之間的數量關系，并利用這個關系解決相關問題．
  （1）如圖一，在等腰△ABC中，AB=AC，BC邊上有一點D，過點D作DE⊥AB于E，DF⊥AC于F，過點C作CG⊥AB于G．利用面積證明：DE+DF=CG．
  （2）如圖二，將矩形ABCD沿著EF折疊，使點A與點C重合，點B落在B'處，點G為折痕EF上一點，過點G作GM⊥FC于M，GN⊥BC于N．若BC=8，BE=3，求GM+GN的長．
  （3）如圖三，在四邊形ABCD中，E為線段BC上的一點，EA⊥AB，ED⊥CD，連接BD，且

  AB

  CD

  =

  AE

  DE

  ，BC=

  51

  ，CD=3，BD=6，求ED+EA的長．
  
  組卷：1640引用：4難度：0.3

  解析