2023-2024學年湖北省知名中小學教聯體聯盟九年級（上）期中數學試卷

一、精心選一選（本大題共8個小題，每小題3分，滿分24分.在每小題給出的四個選

• 1．將一元二次方程2x²+x=3化成一般形式之后，若二次項的系數是2，則一次項系數和常數項分別是（　　）

  A．-1，3

  B．1，1

  C．1，-3

  D．1，3
  組卷：658引用：5難度：0.9

  解析

• 2．下列手機手勢解鎖圖案中，是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：2085引用：76難度：0.9

  解析

• 3．已知函數y=-x²+x,當函數值y隨x的增大而增大時，x的取值范圍是（　　）

  A．x＜ 1 2

  B．x＞ 1 2

  C．x＜- 1 2

  D．x＞- 1 2
  組卷：160引用：2難度：0.5

  解析

• 4．一個QQ群里共有x個好友，每個好友都分別給群里的其他好友發一條信息，共發信息1980條，則可列方程（　　）

  A． 1 2 x（x-1）=1980	B．x（x-1）=1980
  C． 1 2 x（x+1）=1980	D．x（x+1）=1980
  組卷：3007引用：28難度：0.9

  解析

• 5．把拋物線y=5x²向左平移2個單位，再向上平移3個單位，得到的拋物線是（　　）

  A．y=5（x-2）2+3	B．y=5（x+2）2-3
  C．y=5（x+2）2+3	D．y=5（x-2）2-3
  組卷：2601引用：47難度：0.8

  解析

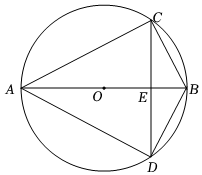• 6．如圖，CD是圓O的弦，直徑AB⊥CD，垂足為E，若AB=12，BE=3，則四邊形ACBD的面積為（　　）

  A．36 3

  B．24 3

  C．18 3

  D．72 3
  組卷：4309引用：22難度：0.7

  解析

• 7．已知二次函數y=x²+bx+c中，其函數y是自變量x之間的部分對應值如下表所示：
  

  x	…	0	1	2	3	…
  y	…	5	2	1	2	…

  點A（x₁，y₁）、B（x₂，y₂）在此函數圖象上，則當0＜x₁＜1，2＜x₂＜3時，y₁與y₂的大小關系正確的是（　　）

  A．y1≥y2

  B．y1＞y2

  C．y1＜y2

  D．y1≤y2．
  組卷：559引用：3難度：0.6

  解析

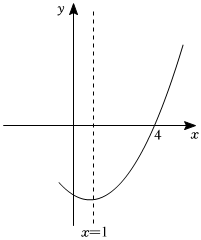• 8．如圖，拋物線y=ax²+bx+c（a≠0）與x軸交于點（4，0），其對稱軸為直線x=1，結合圖象給出下列結論：
  ①abc＞0；
  ②3a+c＜0；
  ③M（-3，y₁），N（3，y₂）是拋物線上兩點，則y₁＜y₂；
  ④若關于x的一元二次方程ax²+bx+c=a-5沒有實數根．則

  0

  ＜

  a

  ＜

  1

  2

  ；
  ⑤對于任意實數m,總有am²+bm-a-b≥0．
  其中正確的結論有（　　）

  A．2個

  B．3個

  C．4個

  D．5個
  組卷：404引用：3難度：0.5

  解析

三、專心解一解（本大題共8小題，滿分72分.請認真讀題，冷靜思考.解答題應寫出必

• 23．小華同學對圖形旋轉前后的線段之間、角之間的關系進行了拓展探究．
  
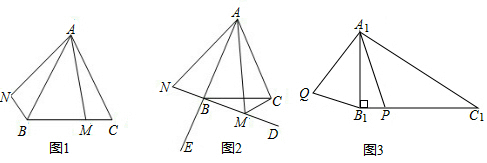
  （一）猜測探究
  在△ABC中，AB=AC，M是平面內任意一點，將線段AM繞點A按順時針方向旋轉與∠BAC相等的角度，得到線段AN，連接NB．
  （1）如圖1，若M是線段BC上的任意一點，請直接寫出∠NAB與∠MAC的數量關系是

  ，NB與MC的數量關系是

  ；
  （2）如圖2，點E是AB延長線上點，若M是∠CBE內部射線BD上任意一點，連接MC，（1）中結論是否仍然成立？若成立，請給予證明，若不成立，請說明理由．
  （二）拓展應用
  如圖3，在△A₁B₁C₁中，A₁B₁=8，∠A₁B₁C₁=90°，∠C₁=30°，P是B₁C₁上的任意點，連接A₁P，將A₁P繞點A₁按順時針方向旋轉60°，得到線段A₁Q，連接B₁Q．求線段B₁Q長度的最小值．
  組卷：1723引用：4難度：0.3

  解析

• 24．如圖，在平面直角坐標系中，拋物線

  y

  =

  1

  2

  x

  2

  +

  bx

  +

  c

  與x軸交于點A（-1，0）、點B，與y軸交于點C，且OC=2，點P是拋物線上一動點．
  （1）求該拋物線的解析式及點B的坐標；
  （2）當點P在第四象限時，求△BCP的最大面積，并求出點P的坐標；
  （3）當點P在拋物線上時，且∠PBA=∠BAC時，求出點P的坐標．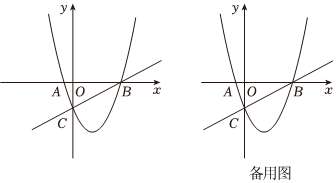
  
  組卷：263引用：1難度：0.1

  解析