2022年浙江省金華市中考數(shù)學(xué)模擬試卷（3月份）

一、選擇題（本題共有10小題，每小題3分，共30分）

• 1．第24屆冬季奧林匹克運(yùn)動(dòng)會在北京市和張家口市聯(lián)合舉行．下面是從歷屆冬奧會的會徽中選取的部分圖形，其中是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：44引用：1難度：0.8

  解析

• 2．預(yù)計(jì)到2025年，中國5G用戶將超過460000000，將460000000用科學(xué)記數(shù)法表示為（　　）

  A．4.6×109

  B．46×107

  C．4.6×108

  D．0.46×109
  組卷：2003引用：58難度：0.9

  解析

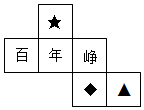• 3．一個(gè)正方體的表面分別標(biāo)有百、年、崢、嶸、歲、月，下面是該正方體的一個(gè)展開圖，已知“嶸”的對面為“歲”，則（　　）

  A．▲代表“歲”

  B．▲代表“月”

  C．★代表“月”

  D．◆代表“月”
  組卷：599引用：9難度：0.7

  解析

• 4．下列說法正確的是（　　）

  A．任意擲一枚質(zhì)地均勻的骰子，擲出的點(diǎn)數(shù)一定是奇數(shù)

  B．“從一副撲克牌中任意抽取一張，抽到大王”是必然事件

  C．了解一批冰箱的使用壽命，采用抽樣調(diào)查的方式

  D．若平均數(shù)相同的甲、乙兩組數(shù)據(jù)，S甲2=3，S乙2=0.02，則甲組數(shù)據(jù)更穩(wěn)定
  組卷：79引用：2難度：0.7

  解析

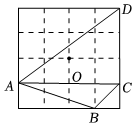• 5．如圖所示，在4×4的網(wǎng)格中，A、B、C、D、O均在格點(diǎn)上，則點(diǎn)O是（　　）

  A．△ABC的內(nèi)心

  B．△ABC的外心

  C．△ACD的外心

  D．△ACD的重心
  組卷：158引用：2難度：0.6

  解析

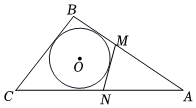• 6．如圖，△ABC周長為20cm,BC=6cm,圓O是△ABC的內(nèi)切圓，圓O的切線MN與AB、CA相交于點(diǎn)M、N，則△AMN的周長為（　　）

  A．14cm

  B．8cm

  C．7cm

  D．9cm
  組卷：1414引用：7難度：0.5

  解析

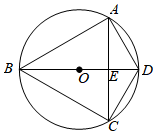• 7．如圖，四邊形ABCD內(nèi)接于直徑為4的⊙O，AB=AC，E是弦AC和直徑BD的交點(diǎn)，ED=

  4

  5

  ，則弦AD的長為（　　）

  A． 3 3

  B． 4 3 3

  C． 2 3

  D． 6
  組卷：666引用：4難度：0.6

  解析

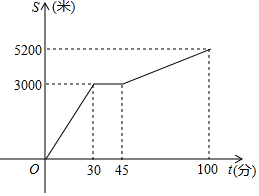• 8．周末小蘭外出爬山，她從山腳爬到山頂?shù)倪^程中，途中休息了一段時(shí)間，設(shè)她從山腳出發(fā)后所用時(shí)間為t（分鐘），所走路程為s（米），s與t之間的函數(shù)關(guān)系如圖所示，下列說法錯(cuò)誤的是（　　）

  A．小蘭途中休息了15分鐘

  B．小蘭爬上山頂所走路程為8200米

  C．小蘭從山腳爬到山頂共用了100分鐘

  D．小蘭休息前的速度大于休息后的速度
  組卷：206引用：2難度：0.7

  解析

三、解答題（本題共有8小題，其中17、18、19每小題0分，20、21每小題0分，22、23每小題0分，24小題12分，共66分）

• 23．方法學(xué)習(xí)
  如圖1，在邊長為1的正方形網(wǎng)格中，連結(jié)格點(diǎn)D，N和E，C，DN和EC相交于點(diǎn)P，求tan∠CPN的值．
  思考：求一個(gè)銳角的三角函數(shù)值，我們往往需要找出（或構(gòu)造出）一個(gè)直角三角形．觀察發(fā)現(xiàn)：∠CPN不在直角三角形中，并且頂點(diǎn)不在格點(diǎn)處，我們可以利用網(wǎng)格畫平行線等方法解決此類問題，比如連接格點(diǎn)M，N，可得MN∥EC，則∠DNM=∠CPN，連接DM，那么∠CPN就變換到格點(diǎn)處，并且恰好在Rt△DMN中．可以方便求出tan∠CPN的值為

  ；
  問題解決
  （1）如圖2，在邊長為1的正方形網(wǎng)格中，AN與CM相交于點(diǎn)P，則cos∠CPN的值為

  ；
  （2）如圖3，在邊長為1的正方形網(wǎng)格中，AN與CM相交于點(diǎn)P，則sin∠CPA的值為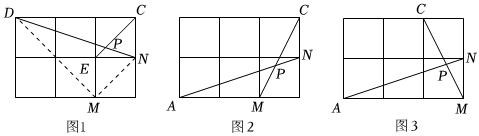

  ；
  
  思維拓展
  如圖4，若干個(gè)形狀、大小完全相同的菱形組成網(wǎng)格，網(wǎng)格頂點(diǎn)稱為格點(diǎn)，已知菱形的較小內(nèi)角為60度，點(diǎn)A，B，C，D都在格點(diǎn)處，線段AB與CD相交于點(diǎn)P求cos∠CPA的值．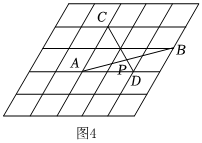
  
  組卷：602引用：5難度：0.1

  解析

• 24．在平面直角坐標(biāo)系中，我們定義直線y=ax-a為拋物線y=ax²+bx+c（a、b、c為常數(shù)，a≠0）的“夢想直線”；有一個(gè)頂點(diǎn)在拋物線上，另有一個(gè)頂點(diǎn)在y軸上的三角形為其“夢想三角形”．已知拋物線y=ax²+bx+c與其“夢想直線”交于A、B兩點(diǎn)（點(diǎn)A在點(diǎn)B的左側(cè)），與x軸負(fù)半軸交于點(diǎn)C，tan∠ABO=

  2

  3

  3

  ，B（1，0），點(diǎn)A橫坐標(biāo)為-2，BC=4．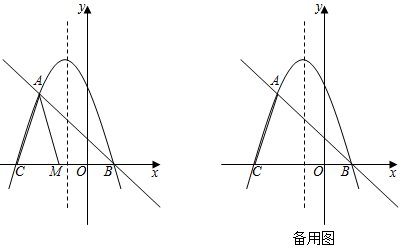
  
  （1）求拋物線的解析式，并寫出頂點(diǎn)坐標(biāo)；
  （2）如圖，點(diǎn)M為線段CB上一動(dòng)點(diǎn)，將△ACM以AM所在直線為對稱軸翻折，點(diǎn)C的對稱點(diǎn)為N，若△AMN為該拋物線的“夢想三角形”，求點(diǎn)N的坐標(biāo)；
  （3）當(dāng)點(diǎn)E在拋物線的對稱軸上運(yùn)動(dòng)時(shí)，在該拋物線的“夢想直線”上，是否存在點(diǎn)F，使得以點(diǎn) A、C、E、F為頂點(diǎn)的四邊形為平行四邊形？若存在，請直接寫出點(diǎn) E、F的坐標(biāo)；若不存在，請說明理由．
  組卷：1002引用：4難度：0.3

  解析