2023年江蘇省泰州市靖江市中考數學二模試卷

一、選擇題（本大題共有6小題，每小題3分，共18分．在每小題所給出的四個選項中，恰有一項是符合題目要求的，請將正確選項的字母代號填涂在答題卡相應位置上）

• 1．下列四個數中，是負數的是（　　）

  A．|-3|

  B．-（-3）

  C．（-3）2

  D．-3
  組卷：350引用：3難度：0.8

  解析

• 2．下列圖形中既是中心對稱圖形又是軸對稱圖形的是（　　）

  A．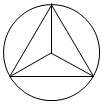

  B．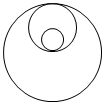

  C．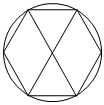

  D．
  組卷：73引用：5難度：0.9

  解析

• 3．下列運算結果錯誤的是（　　）

  A．m3÷m2=m

  B．（m2）3=m6

  C．m2?m3=m5

  D．m2+m3=m5
  組卷：36引用：1難度：0.8

  解析

• 4．在平面直角坐標系中，把一個多邊形的所有頂點坐標（其中有一個頂點為原點、有一條邊在橫坐標軸上）分別乘以-

  1

  2

  所對應的圖形與原圖形是（　　）

  A．位似變換

  B．旋轉變換

  C．軸對稱變換

  D．平移變換
  組卷：56引用：1難度：0.8

  解析

• 5．對于數據：2、2、5、3、7、5、5．下列統計量不能在原數據中找出的是（　　）

  A．極差

  B．平均數

  C．中位數

  D．眾數
  組卷：45引用：3難度：0.6

  解析

• 6．已知拋物線y=-x²-4mx+m²-1，A（-2m-4，y₁），B（m+3，y₂）為該拋物線上的兩點，若y₁＜y₂，則m的取值范圍（　　）

  A．m＜ - 7 3	B．m＞ 1 3
  C．m＜ - 7 3 或m＞ 1 3	D． - 7 3 ＜m＜ 1 3
  組卷：220引用：1難度：0.5

  解析

二、填空題（本大題共有10小題，每小題3分，共30分．請把答案直接填寫在答題卡相應位置上）

• 7．2023年5月6日，“五一”消費數據出爐，國內旅游收入約148000000000元，將數據148000000000用科學記數法表示為

  ．
  組卷：55引用：2難度：0.9

  解析

• 8．二次根式

  x

  -

  4

  中x的取值范圍是

  ．
  組卷：56引用：4難度：0.8

  解析

三、解答題（本大題共有10題，共102分.請在答題卡指定區域內作答，解答時應寫出必要的文字說明、證明過程或演算步驟）

• 25．【問題情境】
  綜合與實踐課上，老師讓同學們以“正方形紙片折疊的方式，探索tan22.5°及tan15°”為主題開展數學活動，下面是同學們的折紙過程．【操作過程】
  （1）如圖1，先將正方形紙片沿對角線折疊，折痕為BD．將點C翻折到BD上的點F處，且使折痕過點B，則∠EBC=∠EBF=22.5°，則tan22.5°=

  ；
  （2）為構造15°，同學們積極動腦并進行如下操作：如圖2，將正方形紙片翻折，使得點A與點D、點B與點C重合，折痕為GH．展開后，將點C翻折到GH上的點R處，且使折痕過點B，連接BR．再將點A翻折到GH上的點R處，折痕為BK．根據以上操作請你求出tan15°的值；
  【探索發現】
  （3）如圖3，在圖2的基礎上，同學們通過其他折疊方式在CD上找到一點P，使得∠PBC=15°，連接KP，發現S_△ABK與S_△DKP存在固定不變的數量關系，請寫出你的猜想并驗證．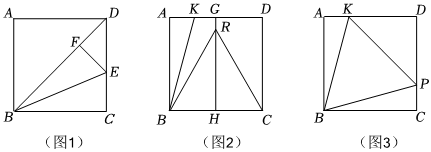
  組卷：123引用：2難度：0.1

  解析

• 26．定義（a,b,c）為函數y=ax²+bx+c的“特征數”．如：函數y=2x²-3x+5的“特征數”是（2，-3，5），函數y=x+2的“特征數”是（0，1，2），函數y=-2x的“特征數”是（0，-2，0）．
  （1）若一個函數y₁的特征數是（0，k,6）（k為常數，且k≠0），將此函數的圖象向下平移6個單位得到一個圖象對應的函數y₂“特征數”是

  ；
  （2）若將一個函數關于y軸對稱得到的對應函數y₃的特征數是（1，-4，3），則原函數的特征數是

  ．
  A．（-1，-4，-3）
  B．（-1，4，-3）
  C．（1，4，3）
  D．（1，4，-3）
  （3）若（2）中對應函數y₃上有兩點A（m+2，n₁），B（2m+1，n₂），其中A在B的左側，當m為整數時，

  n

  2

  n

  1

  也為整數，求m的值；
  （4）若（1）中的函數y₂與（2）中的函數y₃交于C，D兩點，在y軸正半軸上是否存在一點P（0，p），分別與C，D兩點連接，構造特征數是（0，a,p），（0，b,p）的函數，當k取不為0的任意實數時，都能使得a+b為定值．若存在，求出P點坐標及這個定值，若不存在請說明理由．
  組卷：196引用：2難度：0.2

  解析