當前位置：試卷中心 > 試卷詳情

2022年浙江省金華市義烏市中考數學調研試卷

發布：2024/4/20 14:35:0

一、選擇題（本題有10小題，每小題3分，共30分）

1．-2的相反數是（　　）
A．2 B．-2 C．
-
1
2
D．
1
2
組卷：4745引用：1083難度：0.9
解析
2．在平面直角坐標系中，點（-1，2）所在的象限是（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：211引用：21難度：0.9
解析
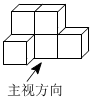3．下列幾何體的俯視圖是（　　）
A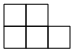． B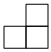． C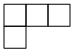． D．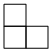
組卷：46引用：1難度：0.9
解析
4．2021年義烏市全體居民人均可支配收入超過7.7萬元．其中7.7萬元用科學記數法表示為（　　）
A．77×10⁴元 B．7.7×10³元 C．7.7×10⁴元 D．0.77×10⁵元
組卷：16引用：2難度：0.7
解析
5．已知a≠0，下列運算中正確的是（　　）
A．a+a²=a³ B．（a³）²÷a²=a⁴
C．（a³）²=a⁵ D．a²?a³=a⁶
組卷：99引用：4難度：0.8
解析
6．已知一個底面半徑為3cm的圓錐，它的母線長是5cm,則這個圓錐的側面積是（　　）cm²．
A．15π B．45π C．30π D．20π
組卷：349引用：4難度：0.7
解析
7．在分析一組數據時，小華列出了方差的計算公式
S
2
=
（
2
-
x
）
2
+
（
3
-
x
）
2
+
（
4
-
x
）
2
+
（
5
-
x
）
2
n
由公式提供的信息，可得出n的值是（　　）
A．2 B．3 C．4 D．5
組卷：122引用：4難度：0.7
解析
8．用配方法解方程x²-8x+1=0時，配方結果正確的是（　　）
A．（x-4）²=5 B．（x-4）²=16 C．（x-4）²=7 D．（x-4）²=15
組卷：218引用：7難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本大題有8小題，共66分，各小題都必須寫出解答過程）

23．在平面直角坐標系中，點P（x₁，y₁）是圖形G₁上的任意一點，點Q（x₂，y₂）是圖形G₂上的任意一點，若存在直線y=kx+b（k≠0）滿足y₁≤kx₁+b且y₂≥kx₂+b,則稱直線l：y=kx+b（k≠0）是圖形G₁與G₂的“分離直線”，例如：如圖1，直線l：y=-x-4是函數圖象與正方形的一條“分離直線”．

（1）在直線y₁=-x,y₂=2x+3，y₃=-2x+3中，是圖1函數
y
=
1
x
（
x
＜
0
）
的圖象與正方形OABC的“分離直線”的為
；
（2）如圖2，第一象限內的等腰Rt△EDF兩腰分別與坐標軸平行，直角頂點D的坐標是
（
3
，
1
）
，過D點的平行四邊形HKMN（D在邊HK上，且不與H，K重合），且HK∥EF，請求出△EDF與平行四邊形HKMN“分離直線”的表達式．
（3）正方形A₁B₁C₁D₁一邊在y軸上，其它三邊都在y軸的左側，且點M（-1，t）是此正方形對角線的交點．若存在直線y=2x+b是
y
=
-
3
x
（
-
4
≤
x
≤
-
1
）
的圖象與正方形A₁B₁C₁D₁的“分離直線”，求t的取值范圍．
組卷：174引用：3難度：0.1
解析
24．如圖，在平面直角坐標系xOy中，菱形OABC的頂點A在x軸的正半軸上，點C的坐標為（3，4），點D從原點O出發沿O→A→B勻速運動，到達點B時停止，點E從點A出發沿A→B→C隨D運動，且始終保持∠CDE=∠COA．設運動時間為t.

（1）當DE∥OB時，求證：△OCD≌△BCE．
（2）若點E在BC邊上，當△CDE為等腰三角形時，求BE的長．
（3）若點D的運動速度為每秒1個單位，是否存在這樣的t,使得以點C，D，E為頂點的三角形與△OCD相似？若存在，直接寫出所有符合條件的t；若不存在，請說明理由．
組卷：212引用：3難度：0.1
解析