2022年遼寧省大連二十四中高考數學模擬試卷（最后一模）
發布：2024/4/20 14:35:0
一、選擇題（本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的）
-
1．已知全集U=R，設集合A={x|x2-x-6≤0}，B={x|x-1＜0}，則A∪（?UB）=（ ）
組卷：193引用：4難度：0.8 -
2．“關于x的方程
=|x-m|（m∈R）有解”的一個必要不充分條件是（ ）1-x2組卷：145引用：2難度：0.8 -
3．公元1715年英國數學家布魯克?泰勒在他的著作中陳述了“泰勒公式”，如果滿足一定的條件，泰勒公式可以用函數在某一點的各階導數值構建一個多項式來近似表達這個函數．泰勒公式將一些復雜函數近似地表示為簡單的多項式函數，使得它成為分析和研究許多數學問題的有力工具，例如：
，其中x∈R，n∈N*，試用上述公式估計ex=+∞∑n=0xnn!=x00!+x11!+x22!+x33!+?+xnn!+?的近似值為（精確到0.001）（ ）e組卷：213引用：2難度：0.6 -
4．中國古代數學的瑰寶《九章算術》中記載了一種稱為“曲池”的幾何體，該幾何體為上、下底面均為扇環形的柱體（扇環是指圓環被扇形截得的部分）．現有一個如圖所示的曲池，其高為3，AA1⊥底面，底面扇環所對的圓心角為，弧π2長度為弧?AD長度的3倍，且CD=2，則該曲池的體積為（ ）?BC組卷：256引用：18難度：0.7 -
5．若離散型隨機變量X的分布列為
，則P（X=k）=m?2k（2k+1-1）（2k-1）（1≤k≤5，k∈Z）的值為（ ）P（32＜x＜52）組卷：368引用：5難度：0.6 -
6．設m∈R，過定點A的動直線x+my=0和過定點B的動直線mx-y-m+3=0交于點P（x,y），（點P與點A，B不重合），則△PAB的面積最大值是（ ）
組卷：924引用：5難度：0.7 -
7．若將函數f（x）=sinx（sinx+cosx）的圖象向左平移
個單位，所得圖象對應的函數在區間（-m,m）上無極值點，則m的最大值為（ ）π4組卷：111引用：1難度：0.6
四、解答題（本題共6小題，共70分.解答應?出文字說明、證明過程或演算步驟）
-
21．某汽車公司最近研發了一款新能源汽車，并在出廠前對100輛汽車進行了單次最大續航里程的測試．現對測試數據進行分析，得到如圖所示的頻率分布直方圖：
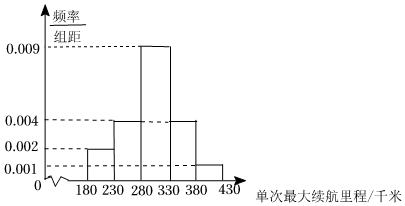
（1）估計這100輛汽車的單次最大續航里程的平均值（同一組中的數據用該組區間的中點值代表）；
（2）經計算第（1）問中樣本標準差S的近似值為50，根據大量的測試數據，可以認為這款汽車的單次最大續航里程X近似地服從正態布N（μ，σ2）（用樣本平均數和標準差s分別作為μ、σ的近似值），現任取一輛汽車，求它的單次最大續航里程X∈[250，400]的概率；x
（參考數據：若隨機變量X～N（μ，σ2），則P（μ-σ≤X≤μ+σ）≈0.6827，P（μ-2σ≤X≤μ+2σ）≈0.9545，P（μ-3σ≤X≤μ+3σ）≈0.9973）
（3）某汽車銷售公司為推廣此款新能源汽車，現面向意向客戶推出“玩游戲，送大獎”活動，客戶可根據拋擲硬幣的結果，操控微型遙控車在方格圖上（方格圖上依次標有數字0、1、2、3、……、20）移動，若遙控車最終停在“勝利大本營”（第19格），則可獲得購車優惠券3萬元；若遙控車最終停在“微笑大本營”（第20格），則沒有任何優惠券．已知硬幣出現正、反面的概率都是，遙控車開始在第0格，客戶每擲一次硬幣，遙控車向前移動一次：若擲出正面，遙控車向前移動一格（從k到k+1）；若擲出反面，遙控車向前移動兩格（從k到k+2），直到遙控車移到“勝利大本營”或“微笑大本營”時，游戲結束．設遙控車移到第n（1≤n≤19）格的概率為Pn，試證明{Pn-Pn-1}是等比數列，并求參與游戲一次的顧客獲得優惠券金額的期望值（精確到0.1萬元）．12組卷：602引用：3難度：0.2 -
22．已知函數f（x）=（2x2-3x）ex，g（x）=alnx（a∈R）．
（1）求f（x）的最小值；
（2）記f'（x）為f（x）的導函數，設函數有且只有一個零點，求a的取值范圍．h（x）=f′（x）2x+3-g（x）組卷：123引用：4難度：0.3