2022-2023學(xué)年湖南師大附中九年級(jí)（上）期末數(shù)學(xué)試卷
發(fā)布：2024/4/20 14:35:0
一、選擇題（本題共10個(gè)小題，每小題3分，共30分）
-
1．2022年10月12日，“天宮課堂”第三課在中國(guó)空間站開講，3名航天員演示了在微重力環(huán)境下毛細(xì)效應(yīng)實(shí)驗(yàn)、水球變“懶”實(shí)驗(yàn)等，相應(yīng)視頻在某短視頻平臺(tái)的點(diǎn)贊量達(dá)到150萬次，數(shù)據(jù)150萬用科學(xué)記數(shù)法表示為（ ）
組卷：1400引用：24難度：0.7 -
2．下列運(yùn)算正確的是（ ）
組卷：426引用：7難度：0.6 -
3．古典園林中的窗戶是中國(guó)傳統(tǒng)建筑裝飾的重要組成部分，一窗一姿容，一窗一景致．下列窗戶圖案中，是中心對(duì)稱圖形的是（ ）
組卷：288引用：22難度：0.9 -
4．二次函數(shù)y=-（x-1）2+3的最大值是（ ）
組卷：709引用：5難度：0.8 -
5．如圖，AB∥CD，∠B=40°，則∠ECD的度數(shù)為（ ）組卷：47引用：6難度：0.9 -
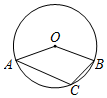6．如圖，A，B，C是⊙O上的三個(gè)點(diǎn)，如果∠AOB=140°，那么∠ACB的度數(shù)為（ ）組卷：424引用：6難度：0.6 -
7．如圖，△ABC與△A'B'C′位似，位似中心為點(diǎn)O，OA'=2AA'，△ABC的周長(zhǎng)為9，則△A'B'C'周長(zhǎng)為（ ）組卷：348引用：6難度：0.6 -
8．明代《算法統(tǒng)宗》有一首飲酒數(shù)學(xué)詩(shī)：“醇酒一瓶醉三客，薄酒三瓶醉一人，共同飲了一十九，三十三客醉顏生，試問高明能算士，幾多醨酒幾多醇？”這首詩(shī)是說：“好酒一瓶，可以醉倒3位客人；薄酒三瓶，可以醉倒1位客人，如今33位客人醉倒了，他們總共飲19瓶酒．試問：其中好酒、薄酒分別是多少瓶？”設(shè)有好酒x瓶，薄酒y瓶．根據(jù)題意，可列方程組為（ ）
組卷：2037引用：10難度：0.7
三、解答題（17、18、19題6分，20、21題8分，22、23題每個(gè)9分，24、25題10分，共計(jì)72分）
-
24．定義：兩個(gè)相似三角形，如果它們的一組對(duì)應(yīng)角有一個(gè)公共的頂點(diǎn)，那么把這兩個(gè)三角形稱為“陽(yáng)似三角形”、如圖1，在△ABC與△AED中，△ABC∽△AED．所以稱△ABC與△AED為“陽(yáng)似三角形”，連接EB，DC，則
為“陽(yáng)似比”．DCEB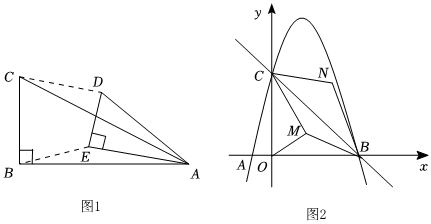
（1）如圖1，已知Rt△ABC與Rt△AED為“陽(yáng)似三角形”，其中∠CBA=∠DEA=90°，當(dāng)∠BAC=30°時(shí)，“陽(yáng)似比”=；DCEB
（2）如圖2，二次函數(shù)y=-x2+3x+4交x軸于點(diǎn)A和B兩點(diǎn)，交y軸于點(diǎn)C．
①點(diǎn)M為直線y=x在第一象限上的一個(gè)動(dòng)點(diǎn)，且△OMB與△CNB為“陽(yáng)似三角形”，連接CM，當(dāng)點(diǎn)N落在二次函數(shù)圖象上時(shí)，求出線段OM的長(zhǎng)度；12
②若點(diǎn)M在以O(shè)為圓心的圓上，CN=3，其他條件不變，求BM+2MC的最小值．34組卷：518引用：1難度：0.3 -
25．若拋物線L：y=ax2+bx+c（a≠0）與直線l：y=kx+m（k≠0）有且只有一個(gè)交點(diǎn)，我們就稱此直線l與拋物線L的相切．直線l叫做拋物線L的切線，交點(diǎn)叫做拋物線L的切點(diǎn)．
（1）若點(diǎn)A為拋物線y=x2-2x+4與y軸的交點(diǎn)，求以點(diǎn)A為切點(diǎn)的該拋物線的切線的解析式；
（2）已知一次函數(shù)y1=2x,二次函數(shù)y2=x2+1，是否存在二次函數(shù)y3=ax2+bx+c,其圖象經(jīng)過點(diǎn)（-3，2），使得直線y1=2x與y2=x2+1，y3=ax2+bx+c都相切于同一點(diǎn)？若存在，求出y3的解析式；若不存在，請(qǐng)說明理由；
（3）已知直線l1：y=k1x+m1（k1≠0）、直線l2：y2=k2x+m2（k2≠0）是拋物線y=-x2+2x+3的兩條切線，當(dāng)l1與l2的交點(diǎn)P的縱坐標(biāo)為5時(shí)，試判斷k1?k2是否為定值，并說明理由．組卷：653引用：1難度：0.3