2022-2023學年山西省晉中市九年級（上）期末數學試卷

一、選擇題（本大題共10個小題，每小題3分，共30分，在每小題給出的四個選項中，只有一項符合題目要求，請選出并在答題卡上將該選項涂黑）

• 1．下列各點中，在反比例函數y=

  6

  x

  的圖象上的是（　　）

  A．（2，3）

  B．（2，-3）

  C．（-2，3）

  D．（-3，2）
  組卷：239引用：10難度：0.8

  解析

• 2．如圖，斷臂維納斯是一尊著名的古希臘大理石雕像，具有嚴格的比例性、藝術性、和諧性，蘊藏著豐富的美學價值．斷臂維納斯雕像是通過故意延長雙腿，使之與身高的比值約為0.618，這一比值能夠引起人們的美感，被認為是建筑和藝術中最理想的比例．這體現了數學中的（　　）

  A．平移

  B．旋轉

  C．中心對稱

  D．黃金分割
  組卷：88引用：2難度：0.7

  解析

• 3．下列一元二次方程中，有兩個相等的實數根的是（　　）

  A．x2-2x+2=0

  B．x2-2x+1=0

  C．x2-2x=0

  D．x2-2x-3=0
  組卷：341引用：4難度：0.7

  解析

• 4．如圖，在菱形ABCD中，對角線AC，BD相交于點O，添加下列條件，能使菱形ABCD成為正方形的是（　　）

  A．AC=BD

  B．AC⊥BD

  C．AD=AB

  D．AC平分∠DAB
  組卷：1365引用：15難度：0.7

  解析

• 5．老舊小區改造是重要的民生工程，與人民群眾的生活息息相關．某縣開展老舊小區改造，2020年投入此項工程的專項資金為1000萬元，2022年投入資金達到1440萬元．設該縣這兩年投入老舊小區改造工程專項資金的年平均增長率為x,根據題意，可列方程（　　）

  A．1000x=1440

  B．1000（1+x）=1440

  C．1000（1+x）2=1440

  D．1000+1000（1+x）+1000（1+x）2=1440
  組卷：93引用：2難度：0.8

  解析

• 6．若點A（-2，y₁）．B（-1，y₂），C（2，y₃）在反比例函數y=-

  4

  x

  的圖象上，則y₁，y₂，y₃的大小關系是（　　）

  A．y1＞y2＞y3

  B．y2＞y3＞y1

  C．y3＞y2＞y1

  D．y2＞y1＞y3
  組卷：211引用：4難度：0.5

  解析

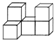• 7．如圖所示的幾何體，其左視圖是（　　）

  A．

  B．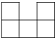

  C．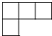

  D．
  組卷：48引用：5難度：0.9

  解析

三、解答題（本大題共8個小題，共75分．解答應寫出必要的文字說明、證明過程或演算步驟．）

• 22．綜合與實踐
  在數學活動課上，同學們對“菱形”進行了深入的探究．實驗材料為同一規格的菱形紙片ABCD，對角線AC，BD相交于點O，對角線AC=12cm,BD=16cm.
  
  （1）如圖1，互助小組發現：若將菱形紙片ABCD沿對角線AC，BD剪開，將△BOC沿BA方向平移，使BC與AD重合，此時拼成的四邊形AODO'為矩形．其判斷的依據是

  ；
  （2）如圖2，奮勇小組發現：將菱形紙片ABCD沿對角線AC剪開，將△ABC繞AC的中點O進行逆時針旋轉，得△A'B'C'，其旋轉角為α，且0°＜α≤90°，連接AA'，A'C，CC'，C'A．試探究四邊形AA'CC'的形狀，并說明理由；
  （3）在（2）的基礎上，博學小組還發現以下兩個結論：
  ①當α=

  時，四邊形AA'CC'為正方形；
  ②如圖3，當點A'正好落在菱形的邊AB上時，A'B=

  cm.
  組卷：121引用：3難度：0.1

  解析

• 23．綜合與探究
  如圖，在矩形OABC中，OA=6，OC=4，分別以AO，OC所在的直線為x軸和y軸建立平面直角坐標系．反比例函數

  y

  =

  k

  x

  （

  x

  ＜

  0

  ）

  的圖象交BC于點E（-2，4），交AB于點F．
  （1）求k的值與點F的坐標；
  （2）在x軸上找一點M，使△EMF的周長最小，并求出點M的坐標；
  （3）在（2）的條件下，若點P是y軸上的一個動點，點Q是平面內的任意一點，試判斷是否存在這樣的點P，使得以點P，Q，M，E為頂點的四邊形是菱形．若存在，請直接寫出點P的坐標；若不存在，請說明理由．
  組卷：629引用：4難度：0.1

  解析